《理論》〈電気及び電子計測〉[H27:問14]整流形の電圧計に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

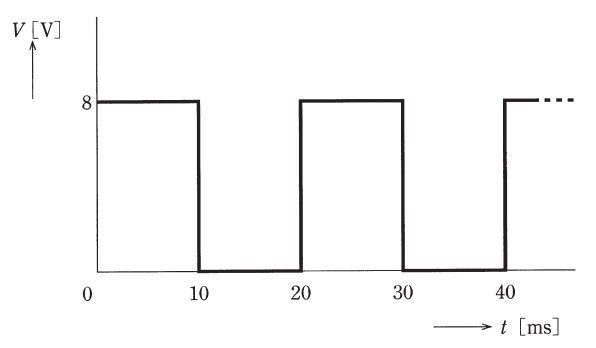
目盛が正弦波交流に対する実効値になる整流形の電圧計(全波整流形)がある。この電圧計で図のような周期\(20 \ \mathrm {ms}\)の繰り返し波形電圧を測定した。

このとき，電圧計の指示の値\(\mathrm {[V]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(4.00\)　　(2)　\(4.44\)　　(3)　\(4.62\)　　(4)　\(5.14\)　　(5)　\(5.66\)

【ワンポイント解説】

電圧計の問題なので，単純に図の実効値を求めてしまうと(5)を選択してしまい間違いとなります。正弦波交流を前提とした電圧計なので，その波形率を考慮し指示値を求める必要があります。

1.全波整流波交流の平均値\(V_{\mathrm {av}}\)と実効値\(V_{\mathrm {e}}\)と波形率\(F\)
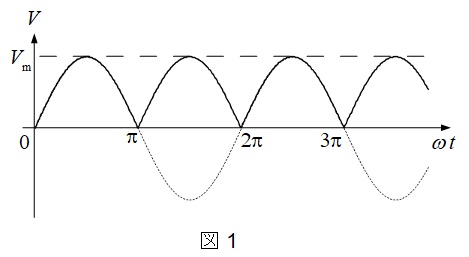
全波整流波交流とは，図1の実線の波形で，平均値\(V_{\mathrm {av}}\)と実効値\(V_{\mathrm {e}}\)，波形率\(F\)は以下のように求められます。
(電験三種の場合は積分の使用を前提としていないため，結果を暗記するしかありません。)
\[
\begin{eqnarray}
V_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }V_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ] &=&\frac {2}{\pi }V_{\mathrm {m}}
\end{eqnarray}
\]

\[
\begin{eqnarray}
V_{\mathrm {e}} &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{V_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\]

\[
\begin{eqnarray}
F &=&\frac {V_{\mathrm {e}}}{V_{\mathrm {av}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {V_{\mathrm {m}}}{\sqrt {2}}}{\displaystyle \frac {2}{\pi }V_{\mathrm {m}}} \\[ 5pt ] &=&\frac {\pi }{2\sqrt {2}} \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　さまざまな交流波形の平均値・実効値まとめ

【解答】

解答：(2)
問題図の電圧の平均値\(V_{\mathrm {av}} \)は，
\[
\begin{eqnarray}
V_{\mathrm {av}} &=&\frac {8\times 10+0\times 10}{20} \\[ 5pt ] &=&4 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，この電圧計は全波整流波交流の波形率を前提として測定値を表示するので，ワンポイント解説「1.全波整流波交流の平均値\(V_{\mathrm {av}}\)と実効値\(V_{\mathrm {e}}\)と波形率\(F\)」より，指示値\(V_{\mathrm {i}}\)は，
\[
\begin{eqnarray}
V_{\mathrm {i}} &=&V_{\mathrm {av}} F \\[ 5pt ] &=&4\times \frac {\pi }{2\sqrt {2}} \\[ 5pt ] &≒&4.44 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。