Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
長さ\( \ 2 \ \mathrm {m} \ \)の直線状の棒磁石があり,その両端の磁極は点磁荷とみなすことができ,その強さは,\(\mathrm {N}\)極が\( \ 1\times 10^{-4} \ \mathrm {Wb} \ \),\(\mathrm {S}\)極が\( \ -1\times 10^{-4} \ \mathrm {Wb} \ \) である。図のように,この棒磁石を点\(\mathrm {BC}\)間に置いた。このとき,点\(\mathrm {A}\)の磁界の大きさの値\( \ \mathrm {[A / m]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,点\(\mathrm {A}\),\(\mathrm {B}\),\(\mathrm {C}\)は,一辺を\( \ 2 \ \mathrm {m} \ \)とする正三角形の各頂点に位置し,真空中にあるものとする。真空の透磁率は\(\mu _{0} = 4\pi \times 10^{-7} \ \mathrm {H / m}\)とする。また,\(\mathrm {N}\)極,\(\mathrm {S}\)極の各点磁荷以外の部分から点\(\mathrm {A}\)への影響はないものとする。
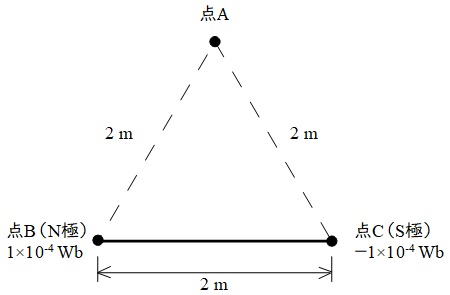
(1) \(0\) (2) \(0.79\) (3) \(1.05\) (4) \(1.58\) (5) \(3.16\)
【ワンポイント解説】
点磁界に関する問題ですが,中身は点電界と全く同じと考えて良いです。点電荷\(Q\)が点磁荷\(m\)となり,電界の強さ\(E\)が磁界の強さ\(H\)になり,真空の誘電率\(\varepsilon _{0}\)が真空の透磁率\(\mu _{0}\)となります。
1.点磁荷におけるクーロンの法則
真空中で距離\(r\)離れた二つの磁荷\(m_{\mathrm {A}}\),\(m_{\mathrm {B}}\)に加わる力\(F\)は,真空の透磁率を\(\mu _{0}\)とすると,
\[
\begin{eqnarray}
F &=&\frac {m_{\mathrm {A}}m_{\mathrm {B}}}{4\pi\mu _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.点磁荷における磁界の大きさ\(H\)
電荷\(m\)から\(r\)離れた点における磁界の強さ\(H\)は,
\[
\begin{eqnarray}
H&=&\frac {m}{4\pi \mu _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(4)
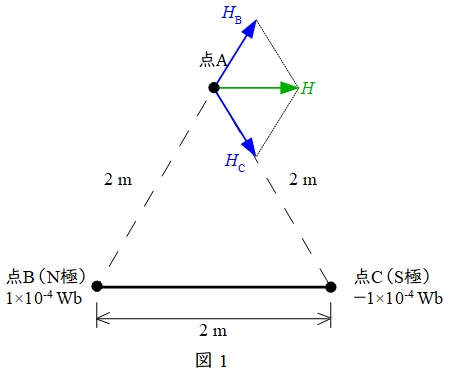
点\(\mathrm {A}\)における磁界の大きさを表すベクトル図を図1に示す。
図1において,点\(\mathrm {B}\)の磁荷\( \ 1\times 10^{-4} \ \mathrm {Wb} \ \)による磁界の大きさ\(H_{\mathrm {B}}\)は,ワンポイント解説「2.点磁荷における磁界の大きさ\(H\)」の通り,
\[
\begin{eqnarray}
H_{\mathrm {B}}&=&\frac {m}{4\pi \mu _{0}r^{2}} \\[ 5pt ]
&=&\frac {1\times 10^{-4}}{4\pi \times 4\pi \times 10^{-7}\times 2^{2}} \\[ 5pt ]
&≒&1.58 \ \mathrm {[A / m]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,点\(\mathrm {C}\)の磁荷\( \ -1\times 10^{-4} \ \mathrm {Wb} \ \)による磁界の大きさ\(H_{\mathrm {C}}\)も全く同じ大きさとなる。
よって,図1の通り,\(H_{\mathrm {B}}\),\(H_{\mathrm {C}}\)が正三角形の辺となっていることから,その合成磁界\(H\)の大きさも\(H_{\mathrm {B}}\)と等しくなる。
したがって,\(H=1.58 \ \mathrm {[A / m]}\)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは