《理論》〈電気回路〉[H26:問9]LC直列回路の共振周波数に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

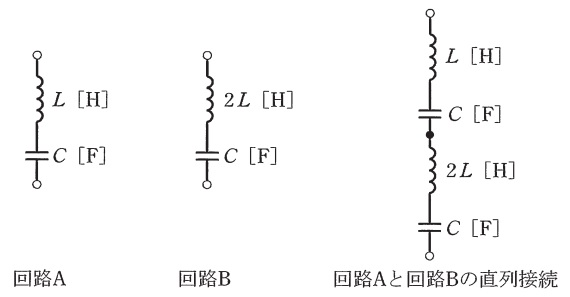
図のように，二つの\( \ LC \ \)直列共振回路\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)があり，それぞれの共振周波数が\( \ f_{\mathrm {A}} \ \mathrm {[Hz]} \ \)，\( \ f_{\mathrm {B}} \ \mathrm {[Hz]} \ \)である。これら\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)をさらに直列に接続した場合，全体としての共振周波数が\( \ f_{\mathrm {AB}} \ \mathrm {[Hz]} \ \)になった。\( \ f_{\mathrm {A}} \ \)，\( \ f_{\mathrm {B}} \ \)，\( \ f_{\mathrm {AB}} \ \)の大小関係として，正しいものを次の(1)～(5)のうちから一つ選べ。

(1)　\( \ f_{\mathrm {A}}＜f_{\mathrm {B}}＜f_{\mathrm {AB}} \ \)　　(2)　\( \ f_{\mathrm {A}}＜f_{\mathrm {AB}}＜f_{\mathrm {B}} \ \)　　(3)　\( \ f_{\mathrm {AB}}＜f_{\mathrm {A}}＜f_{\mathrm {B}} \ \)
(4)　\( \ f_{\mathrm {AB}}＜f_{\mathrm {B}}＜f_{\mathrm {A}} \ \)　　(5)　\( \ f_{\mathrm {B}}＜f_{\mathrm {AB}}＜f_{\mathrm {A}} \ \)

【ワンポイント解説】

直列回路の共振条件は非常に重要な概念となるので，どうしてそうなるのかも含め，必ず算出できるようにしておきましょう。

1.直列回路の共振回路
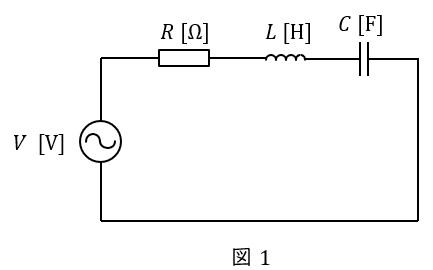
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は，角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.並列回路の共振回路
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \mathrm {[S]} \ \)は，角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　直列共振回路の理論

【解答】

解答：(5)
ワンポイント解説「1.直列回路の共振回路」の通り，回路\( \ \mathrm {A} \ \)の共振周波数\( \ f_{\mathrm {A}} \ \)は，
\[
\begin{eqnarray}
f_{\mathrm {A}}&=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] であり，回路\( \ \mathrm {B} \ \)の共振周波数\( \ f_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
f_{\mathrm {B}}&=&\frac {1}{2\pi \sqrt {2LC}} \\[ 5pt ] &=&\frac {1}{2\sqrt {2}\pi \sqrt {LC}} \\[ 5pt ] &≒&\frac {1}{2.83\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となる。さらに，\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)を直列接続した場合，合成インダクタンスが\( \ 2L+L=3L \ \mathrm {[H]} \ \)，合成静電容量が\( \ \displaystyle \frac {C\cdot C}{C+C}=\frac {C}{2} \ \)となるから，共振周波数\( \ f_{\mathrm {AB}} \ \)は，
\[
\begin{eqnarray}
f_{\mathrm {AB}} &=&\frac {1}{\displaystyle 2\pi \sqrt {3L\cdot \frac {C}{2}}} \\[ 5pt ] &=&\frac {1}{\displaystyle 2\pi \sqrt {\frac {3}{2}LC }} \\[ 5pt ] &=&\frac {1}{\displaystyle 2\sqrt {\frac {3}{2}}\pi \sqrt {LC }} \\[ 5pt ] &≒&\frac {1}{2.45\pi \sqrt {LC}}
\end{eqnarray}
\] となるので，大小関係は\( \ f_{\mathrm {B}}＜f_{\mathrm {AB}}＜f_{\mathrm {A}} \ \)と求められる。