Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
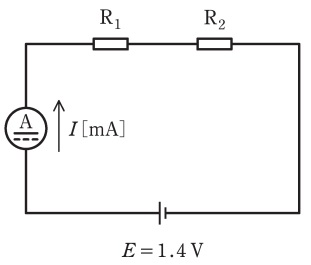
\(\mathrm {R}_{\mathrm {a}}\),\(\mathrm {R}_{\mathrm {b}}\)及び\(\mathrm {R}_{\mathrm {c}}\)の三つの抵抗器がある。これら三つの抵抗器から二つの抵抗器(\(\mathrm {R}_{1}\)及び\(\mathrm {R}_{2}\))を選び,図のように,直流電流計及び電圧\(E=1.4 \ \mathrm {V}\)の直流電源を接続し,次のような実験を行った。
実験Ⅰ:\(\mathrm {R}_{1}\)を\(\mathrm {R}_{\mathrm {a}}\),\(\mathrm {R}_{2}\)を\(\mathrm {R}_{\mathrm {b}}\)としたとき、電流\(I\)の値は\( \ 56 \ \mathrm {mA} \ \)であった。
実験Ⅱ:\(\mathrm {R}_{1}\)を\(\mathrm {R}_{\mathrm {b}}\),\(\mathrm {R}_{2}\)を\(\mathrm {R}_{\mathrm {c}}\)としたとき、電流\(I\)の値は\( \ 35 \ \mathrm {mA} \ \)であった。
実験Ⅲ:\(\mathrm {R}_{1}\)を\(\mathrm {R}_{\mathrm {a}}\),\(\mathrm {R}_{2}\)を\(\mathrm {R}_{\mathrm {c}}\)としたとき、電流\(I\)の値は\( \ 40 \ \mathrm {mA} \ \)であった。
これらのことから,\(\mathrm {R}_{\mathrm {b}}\)の抵抗値\([\Omega ]\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,直流電源及び直流電流計の内部抵抗は無視できるものとする。
(1) \(10\) (2) \(15\) (3) \(20\) (4) \(25\) (5) \(30\)
【ワンポイント解説】
オームの法則以外特別な公式を使用する必要がないため,電験としては易しい問題となると思います。電験では連立方程式は三つの変数までは解ける前提として出題されます。できるだけ早く解けるように問題演習を繰り返して下さい。
【解答】
解答:(2)
実験Ⅰにおける回路方程式より,
\[
\begin{eqnarray}
\left( \mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {b}}\right) I_{1}&=&E \\[ 5pt ]
\mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {b}}&=&\frac {E}{I_{1}} \\[ 5pt ]
\mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {b}}&=&\frac {1.4}{0.056} \\[ 5pt ]
\mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {b}}&=&25 ・・・・・・・・・① \\[ 5pt ]
\end{eqnarray}
\]
が導かれ,同様に実験Ⅱ,Ⅲより,
\[
\begin{eqnarray}
\left( \mathrm {R}_{\mathrm {b}}+\mathrm {R}_{\mathrm {c}}\right) I_{2}&=&E \\[ 5pt ]
\mathrm {R}_{\mathrm {b}}+\mathrm {R}_{\mathrm {c}}&=&\frac {E}{I_{2}} \\[ 5pt ]
\mathrm {R}_{\mathrm {b}}+\mathrm {R}_{\mathrm {c}}&=&\frac {1.4}{0.035} \\[ 5pt ]
\mathrm {R}_{\mathrm {b}}+\mathrm {R}_{\mathrm {c}}&=&40 ・・・・・・・・・② \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\left( \mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {c}}\right) I_{3}&=&E \\[ 5pt ]
\mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {c}}&=&\frac {E}{I_{3}} \\[ 5pt ]
\mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {c}}&=&\frac {1.4}{0.040} \\[ 5pt ]
\mathrm {R}_{\mathrm {a}}+\mathrm {R}_{\mathrm {c}}&=&35 ・・・・・・・・・③ \\[ 5pt ]
\end{eqnarray}
\]
が導かれる。\(①-③\)より,
\[
\begin{eqnarray}
\mathrm {R}_{\mathrm {b}}-\mathrm {R}_{\mathrm {c}}&=&-10 ・・・・・・・・・④ \\[ 5pt ]
\end{eqnarray}
\]
となるから,\(②+④\)より,
\[
\begin{eqnarray}
2\mathrm {R}_{\mathrm {b}}&=&30 \\[ 5pt ]
\mathrm {R}_{\mathrm {b}}&=&15 \ [\Omega ] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは