《理論》〈電気回路〉[R05下:問5]直流回路において未知の抵抗で消費される電力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

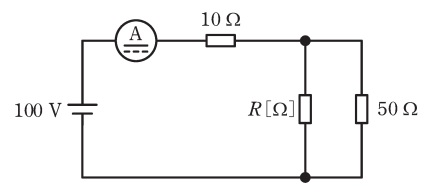
図に示す直流回路は，\( \ 100 \ \mathrm {V} \ \)の直流電圧源に直流電流計を介して\( \ 10 \ \mathrm {\Omega } \ \)の抵抗が接続され，\( \ 50 \ \mathrm {\Omega } \ \)の抵抗と抵抗\( \ R \ \mathrm {[\Omega ]} \ \)が接続されている。電流計は\( \ 5 \ \mathrm {A} \ \)を示している。抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費される電力の値\( \ \mathrm {[W]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。なお，電流計の内部抵抗は無視できるものとする。

　(1)　\( \ 2 \ \)　　(2)　\( \ 10 \ \)　　(3)　\( \ 20 \ \)　　(4)　\( \ 100 \ \)　　(5)　\( \ 200 \ \)　　

【ワンポイント解説】

キルヒホッフの法則を駆使しながら，抵抗値，抵抗に流れる電流，電圧を求めていく問題です。
ステップはありますが，基本的な公式を理解し順序立てて解くようにしましょう。
本問は令和元年問6からの再出題となります。

1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが，法則を説明できる必要はなく，計算で使いこなせることが重要です。
①第1法則（電流則）
　回路の接続点に流入する電流の和と流出する電流の和が等しい。

　図1で言えば，例えば接続点\( \ \mathrm {A} \ \)において，
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ] \end{eqnarray}
\] 　となります。

②第2法則（電圧則）
　任意の閉回路において，起電力の総和と抵抗の電圧降下の和は等しい。

　図1で言えば，例えば閉回路\( \ 1 \ \)において，
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ] \end{eqnarray}
\] 　となります。

2.抵抗での消費電力
ある抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に電圧\( \ V \ \mathrm {[V]} \ \)をかけたとき抵抗に電流\( \ I \ \mathrm {[A]} \ \)が流れたとすると，\( \ R \ \mathrm {[\Omega ]} \ \)での消費電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&VI \\[ 5pt ] \end{eqnarray}
\] となります。オームの法則\( \ V=RI \ \)より上式は，
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ] &=&\frac {V^{2}}{R} \\[ 5pt ] \end{eqnarray}
\] と変形できます。

【関連する「電気の神髄」記事】

　　キルヒホッフの法則とその解釈

【解答】

解答：(5)
\( \ 10 \ \mathrm {\Omega } \ \)の抵抗に流れる電流\( \ I_{10}=5 \ \mathrm {[A]} \ \)であるから，\( \ 10 \ \mathrm {\Omega } \ \)の抵抗にかかる電圧\( \ V_{10} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{10}&=&10\times I_{10} \\[ 5pt ] &=&10\times 5 \\[ 5pt ] &=&50 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R \ \mathrm {[\Omega ]} \ \)及び\( \ 50 \ \mathrm {\Omega } \ \)にかかる電圧は\( \ 100-50=50 \ \mathrm {[V]} \ \)となる。
これより，\( \ 50 \ \mathrm {\Omega } \ \)の抵抗に流れる電流\( \ I_{50} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{50}&=&\frac {50}{50} \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)は，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
I_{\mathrm {R}}&=&5-1 \\[ 5pt ] &=&4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
R&=&\frac {50}{I_{\mathrm {R}}} \\[ 5pt ] &=&\frac {50}{4} \\[ 5pt ] &=&12.5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.抵抗での消費電力」より，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費される電力\( \ P_{\mathrm {R}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {R}}&=&RI_{\mathrm {R}}^{2} \\[ 5pt ] &=&12.5\times 4^{2} \\[ 5pt ] &=&200 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※解説では\( \ R \ \mathrm {[\Omega ]} \ \)を導出していますが，
\[
\begin{eqnarray}
P_{\mathrm {R}}&=&V_{50}I_{\mathrm {R}} \\[ 5pt ] &=&50\times 4 \\[ 5pt ] &=&200 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] でも正答となります。