Contents
【問題】
【難易度】★★★☆☆(普通)
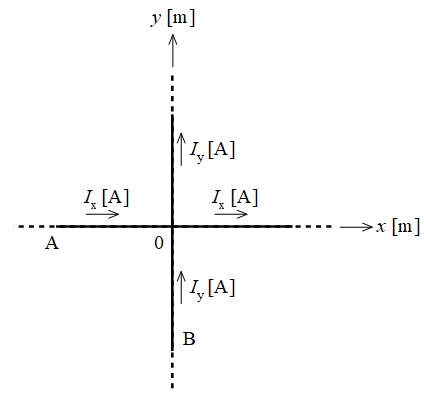
図のように,十分に長い直線状導体\(\mathrm {A}\),\(\mathrm {B}\)があり,\(\mathrm {A}\)と\(\mathrm {B}\)はそれぞれ直角座標系の\(x\)軸と\(y\)軸に沿って置かれている。\(\mathrm {A}\)には\(+x\)方向の電流\(I_{\mathrm {x}} \ \mathrm {[A]}\)が,\(\mathrm {B}\)には\(+y\)方向の電流\(I_{\mathrm {y}} \ \mathrm {[A]}\)が,それぞれ流れている。\(I_{\mathrm {x}} > 0,I_{\mathrm {y}} > 0\)とする。
このとき,\(xy\)平面上で\(I_{\mathrm {x}}\)と\(I_{\mathrm {y}}\)のつくる磁界が零となる点( \(x \ \mathrm {[m]}\),\(y \ \mathrm {[m]}\) )の満たす条件として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,\(x≠0\),\(y≠0\)とする。
(1) \(\displaystyle y=\frac {I_{\mathrm {x}}}{I_{\mathrm {y}}}x\) (2) \(\displaystyle y=\frac {I_{\mathrm {y}}}{I_{\mathrm {x}}}x\) (3) \(\displaystyle y=-\frac {I_{\mathrm {x}}}{I_{\mathrm {y}}}x\)
(4) \(\displaystyle y=-\frac {I_{\mathrm {y}}}{I_{\mathrm {x}}}x\) (5) \(y=±x\)
【ワンポイント解説】
それぞれの電流が作る磁界を分けて考えることが肝となります。あとは,右ねじの法則とアンペールの周回積分の法則を使用して,計算間違いしないように解いて下さい。
1.アンペールの周回積分の法則
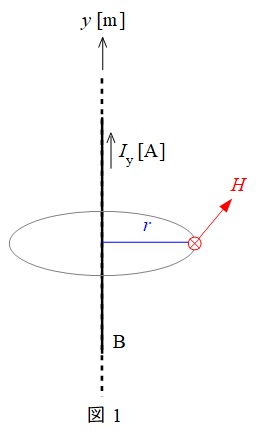
図1のように無限長直線電流\( \ I \ \)が流れているとき,電線から距離\( \ r \ \)の位置での磁界の強さ\( \ H \ \)は,
\[
\begin{eqnarray}
H&=&\frac {I}{2\pi r}
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
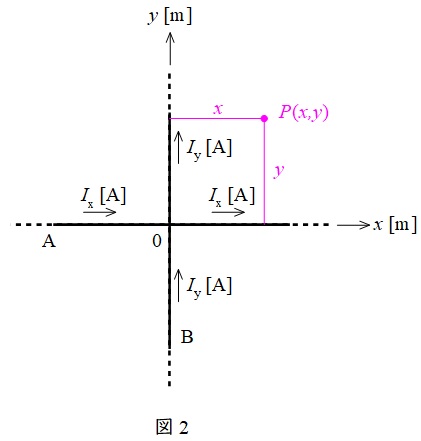
図2のように任意の点\(\mathrm {P}(x,y)\)の磁界の大きさを求める。
ワンポイント解説「1.アンペールの周回積分の法則」より,\(I_{\mathrm {x}}\)が作る磁界の大きさ\(H_{\mathrm {x}}\)は,
\[
H_{\mathrm {x}}=\frac {I_{\mathrm {x}}}{2\pi y} (奥から手前)
\]
であり,\(I_{\mathrm {y}}\)が作る磁界の大きさ\(H_{\mathrm {y}}\)は,
\[
H_{\mathrm {y}}=\frac {I_{\mathrm {y}}}{2\pi x} (手前から奥)
\]
である。よって,磁界の大きさが零となるためには,\(H_{\mathrm {x}}=H_{\mathrm {y}}\)である必要があるため,
\[
\begin{eqnarray}
\frac {I_{\mathrm {x}}}{2\pi y}&=&\frac {I_{\mathrm {y}}}{2\pi x} \\[ 5pt ]
y&=&\frac {I_{\mathrm {x}}}{I_{\mathrm {y}}}x \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは