《理論》〈電気回路〉[R01:問10]時定数と消費されるエネルギーに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

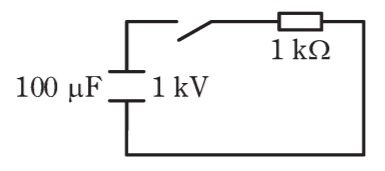
図のように，電圧\( \ 1 \ \mathrm {kV} \ \)で充電された静電容量\( \ 100 \ \mathrm {\mu F} \ \)のコンデンサ，抵抗\( \ 1 \ \mathrm {k\Omega } \ \)，スイッチからなる回路がある。スイッチを閉じた直後に過渡的に流れる電流の時定数\( \ \tau \ \)の値\( \ \mathrm {[s]} \ \)と，スイッチを閉じてから十分に時間が経過するまでに抵抗で消費されるエネルギー\( \ W \ \)の値\( \ \mathrm {[J]} \ \)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccc}
& \tau & W \\
\hline
(1) & 　0.1　 & 　0.1　 \\
\hline
(2) & 　0.1　 & 　50　 \\
\hline
(3) & 　0.1　 & 　1000　 \\
\hline
(4) & 　10　 & 　0.1　 \\
\hline
(5) & 　10　 & 　50　 \\
\hline
\end{array}
\]

【ワンポイント解説】

時定数の公式とコンデンサに蓄えられるエネルギーの２つの公式を理解しているかを問う問題となっています。公式を知っていれば解ける問題なので，それほど難しい内容ではない問題となります。

1.時定数
コンデンサの電圧の導出は微分方程式の計算を伴うため二種以上の範囲となりますが，問題のような回路が与えられると，コンデンサ電圧\( \ V_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {C}} &=&V_{0}\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ] \end{eqnarray}
\] で与えられ，\( \ t=CR \ \)となる時間を時定数と呼びます。

2.コンデンサに蓄えられるエネルギー\( \ W \ \)
静電容量\( \ C \ \)のコンデンサを電圧\( \ V \ \)の電源に接続し，十分に時間が経過した際に，コンデンサに蓄えられるエネルギー\( \ W \ \)は，
\[
\begin{eqnarray}
W&=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(2)
ワンポイント解説「1.時定数」の通り，問題の回路の時定数\( \ \tau \ \)は，
\[
\begin{eqnarray}
\tau &=&CR \\[ 5pt ] &=&100\times 10^{-6}\times 1\times 10^{3} \\[ 5pt ] &=&0.1 \ \mathrm {[s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。
一方，抵抗で消費されるエネルギーは，コンデンサに蓄えられたエネルギーがすべて抵抗で消費されるので，ワンポイント解説「2.コンデンサに蓄えられるエネルギー\( \ W \ \)」の通り，
\[
\begin{eqnarray}
W&=&\frac {1}{2}CV^{2} \\[ 5pt ] &=&\frac {1}{2}\times 100\times 10^{-6}\times \left( 1\times 10^{3}\right) ^{2} \\[ 5pt ] &=&50 \ \mathrm {[J]} \\[ 5pt ] \end{eqnarray}
\] と求められる。