【問題】
【難易度】★★★★☆(やや難しい)
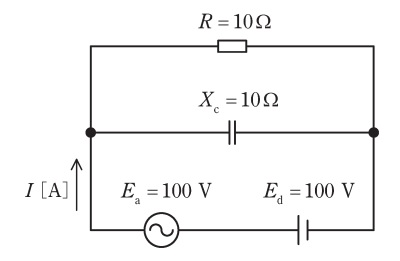
図の回路において,正弦波交流電源と直流電源を流れる電流\( \ I \ \)の実効値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,\( \ E_{\mathrm {a}} \ \)は交流電圧の実効値\( \ \mathrm {[V]} \ \),\( \ E_{\mathrm {d}} \ \)は直流電圧の大きさ\( \ \mathrm {[V]} \ \),\( \ X_{\mathrm {C}} \ \)は正弦波交流電源に対するコンデンサの容量性リアクタンスの値\( \ \mathrm {[\Omega ]} \ \),\( \ R \ \)は抵抗値\( \ \mathrm {[\Omega ]} \ \)とする。
(1) \(10.0\) (2) \(14.1\) (3) \(17.3\) (4) \(20.0\) (5) \(40.0\)
【ワンポイント解説】
重ね合わせの理及び直流と交流の組合せとなるので三平方の定理を用いる必要があります。
1.合成インピーダンス
インピーダンス\( \ {\dot Z}_{1} \ \)と\( \ {\dot Z}_{2} \ \)が与えられている時,それぞれの合成抵抗\( \ {\dot Z} \ \)は以下の式で与えられます。
①直列
直列合成インピーダンス\( \ {\dot Z} \ \)は,
\[
\begin{eqnarray}
{\dot Z}&=&{\dot Z}_{1}+{\dot Z}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成インピーダンス\( \ {\dot Z} \ \)は,
\[
\begin{eqnarray}
\frac {1}{{\dot Z}}&=&\frac {1}{{\dot Z}_{1}}+\frac {1}{{\dot Z}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
{\dot Z}&=&\frac {{\dot Z}_{1}{\dot Z}_{2}}{{\dot Z}_{1}+{\dot Z}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.重ね合わせの理
複数の電源で構成された回路は,電源毎に計算した電流を重ね合わせて求めることができます。この時,電圧源は短絡,電流源は開放します。本問の場合,直流と交流の組合せですが,どちらも電圧源なので短絡することになります。
【関連する「電気の神髄」記事】
【解答】
解答:(3)
重ね合わせの理より,直流電源と交流電源を分けて考える。まず,直流電源においては,定常状態においてコンデンサに流れる電流は零であるから,抵抗分のみ考えればよい。したがって,直流電源により回路を流れる電流\( \ I_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {d}}&=&\frac {E_{\mathrm {d}}}{R} \\[ 5pt ]
&=&\frac {100}{10} \\[ 5pt ]
&=&10 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,交流電源においては,\( \ X_{\mathrm {C}} \ \)と\( \ R \ \)の並列回路となるから,その合成インピーダンス\( {\dot Z} \ \)は,ワンポイント解説「1.合成インピーダンス」の通り,
\[
\begin{eqnarray}
\dot Z&=&\frac {R\cdot \left( -\mathrm {j}X_{\mathrm {C}}\right) }{R-\mathrm {j}X_{\mathrm {C}}} \\[ 5pt ]
&=&\frac {10\cdot \left( -\mathrm {j}10\right) }{10-\mathrm {j}10} \\[ 5pt ]
&=&-\frac {\mathrm {j}100}{10-\mathrm {j}10} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ Z \ \)は,
\[
\begin{eqnarray}
Z&=&\frac {100}{\sqrt {10^{2}+10^{2}}} \\[ 5pt ]
&=&\frac {100}{10\sqrt {2}} \\[ 5pt ]
&=&\frac {10}{\sqrt {2}} \\[ 5pt ]
&=&\frac {10\sqrt {2}}{2} \\[ 5pt ]
&=&5\sqrt {2} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,交流電源により回路を流れる電流\( \ I_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\frac {E_{\mathrm {a}}}{Z} \\[ 5pt ]
&=&\frac {100}{5\sqrt {2}} \\[ 5pt ]
&=&\frac {20}{\sqrt {2}} \\[ 5pt ]
&=&\frac {20\sqrt {2}}{2} \\[ 5pt ]
&=&10\sqrt {2} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。直流と交流の直交性により,それぞれを重ね合わせた電流\( \ I \ \)は,
\[
\begin{eqnarray}
I&=&\sqrt {I_{\mathrm {d}}^{2}+I_{\mathrm {a}}^{2}} \\[ 5pt ]
&=&\sqrt {10^{2}+\left( 10\sqrt {2}\right) ^{2}} \\[ 5pt ]
&=&\sqrt {100+200} \\[ 5pt ]
&=&\sqrt {300} \\[ 5pt ]
&=&10\sqrt {3} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは