《理論》〈電気回路〉[R05下:問6]直流回路における抵抗に加わる端子電圧に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

図のような直流回路において，抵抗\( \ 6 \ \mathrm {\Omega } \ \)の端子間電圧の大きさ\( \ V \ \)の値\( \ \mathrm {[V]} \ \)として，正しいものを次の(1)～(5)のうちから一つ選べ。

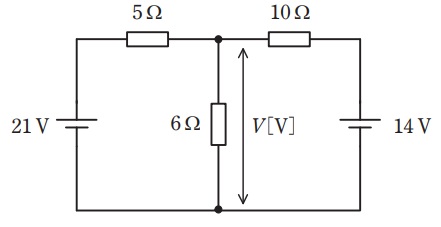
　(1)　\( \ 2 \ \)　　(2)　\( \ 5 \ \)　　(3)　\( \ 7 \ \)　　(4)　\( \ 12 \ \)　　(5)　\( \ 15 \ \)　　

【ワンポイント解説】

直流回路の端子電圧を求める問題です。
本解説ではミルマンの定理を使用して解説していますが，キルヒホッフの法則や重ね合わせの理等様々な解き方が考えられます。ミルマンの定理が最もすっきりして解けると思いますが，試験本番ではある程度強引にでもなんとか正答を導き出していく能力も大事です。
本問は平成15年問5からの再出題となります。

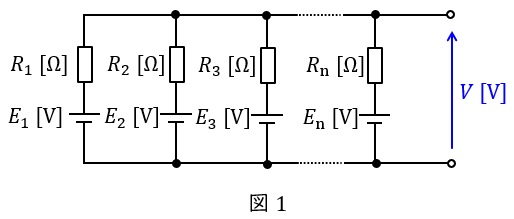
1.ミルマンの定理
図1のような，電源\( \ E_{1} \ \mathrm {[V]} \ \)，\( \ E_{2} \ \mathrm {[V]} \ \)，\( \ \cdots \ \)，\( \ E_{\mathrm {n}} \ \mathrm {[V]} \ \)と抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)，\( \ R_{2} \ \mathrm {[\Omega ]} \ \)，\( \ \cdots \ \)，\( \ R_{\mathrm {n}} \ \mathrm {[\Omega ]} \ \)が直並列された回路における全体の電圧\( \ V \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}}+\frac {E_{3}}{R_{3}}+\cdots +\frac {E_{\mathrm {n}}}{R_{\mathrm {n}}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}}+\cdots +\frac {1}{R_{\mathrm {n}}}} \\[ 5pt ] \end{eqnarray}
\] で求められます。電源が繋がっていない場合は\( \ E=0 \ \mathrm {[V]} \ \)，電源が逆向きの場合は\( \ -E \ \mathrm {[V]} \ \)とすればミルマンの定理はそのまま適用できます。

【解答】

解答：(4)
回路にミルマンの定理を適用すると，ワンポイント解説「1.ミルマンの定理」の通り，
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {21}{5}+\frac {0}{6}+\frac {14}{10}}{\displaystyle \frac {1}{5}+\frac {1}{6}+\frac {1}{10}} \\[ 5pt ] &=&\frac {\displaystyle \frac {42+14}{10}}{\displaystyle \frac {6+5+3}{30}} \\[ 5pt ] &=&\frac {56\times 30}{10\times 14} \\[ 5pt ] &=&12 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。