《理論》〈電磁気〉[R4上:問1]平行板コンデンサの特性と各パラメータの関係に関する論説問題

【問題】

【難易度】★★★☆☆（普通）

面積がともに$\ S \ \mathrm {[m^{2}]} \ $で円形の二枚の電極板（導体平板）を，互いの中心が一致するように間隔$\ d \ \mathrm {[m]} \ $で平行に向かい合わせて置いた平行板コンデンサがある。電極板間は誘電率$\ \varepsilon \ \mathrm {[F / m]} \ $の誘電体で一様に満たされ，電極板間の電位差は電圧$\ V \ \mathrm {[V]} \ $の直流電源によって一定に保たれている。この平行板コンデンサに関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。

ただし，コンデンサの端効果は無視できるものとする。

(1)　誘電体内の等電位面は，電極板と誘電体の境界面に対して平行である。

(2)　コンデンサに蓄えられる電荷量は，誘電率が大きいほど大きくなる。

(3)　誘電体内の電界の大きさは，誘電率が大きいほど小さくなる。

(4)　誘電体内の電束密度の大きさは，電極板の単位面積当たりの電荷量の大きさに等しい。

(5)　静電エネルギーは誘電体内に蓄えられ，電極板の面積を大きくすると静電エネルギーは増大する。

【ワンポイント解説】

平行板コンデンサの特徴に関する問題です。
一見計算もなく易しそうに見える問題ですが，サッと見てしまうと間違いに気づきにくい問題です。
特に今回の誤りに選択肢の内容は平行板コンデンサの特性として非常に重要となる内容なので、公式と合わせて理解しておくようにしましょう。

1.電荷$\ Q \ $と静電容量$\ C \ $及び電圧$\ V \ $の関係
平行平板コンデンサにおいて，蓄えられる電荷$\ Q \ $と静電容量$\ C \ $及び電圧$\ V \ $には，

$$\begin{eqnarray} Q &=&CV \\[ 5pt ] \end{eqnarray}$$ の関係があります。

2.平行平板コンデンサの静電容量$\ C \ $
平板間の誘電率を$\ \varepsilon \ $，平板の面積を$\ S \ $，平板間の間隔を$\ d \ $とすると，静電容量$\ C \ $は，

$$\begin{eqnarray} C &=&\frac {\varepsilon S}{d} \\[ 5pt ] \end{eqnarray}$$ で求められます。

3.平行平板コンデンサの電界$\ E \ $と電圧$\ V \ $の関係
極板間の距離$\ d \ $の平行平板コンデンサに電圧$\ V \ $をかけると，極板間の電界$\ E \ $は，

$$\begin{eqnarray} E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}$$ となります。

4.平行平板コンデンサの電束密度$\ D \ $と電界$\ E \ $の関係
極板間の誘電率を$\ \varepsilon \ $とすると，電束密度$\ D \ $と電界$\ E \ $には，

$$\begin{eqnarray} D&=&\varepsilon E \\[ 5pt ] \end{eqnarray}$$ の関係があります。

5.平行平板コンデンサの静電エネルギー$\ W \ $
平行平板コンデンサの静電エネルギー$\ W \ $は，

$$\begin{eqnarray} W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}$$ であり，$\ Q=CV \ $の関係から，
$$\begin{eqnarray} W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}$$ となります。

【解答】

解答：(3)
(1)：正しい
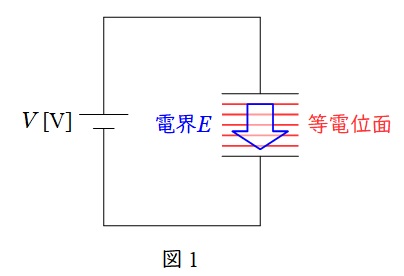
図1に示すように，平行板コンデンサ内（誘電体内）は電界が一様に発生しているため，平行板コンデンサ内（誘電体内）の等電位面は電極板と平行になります。

(2)：正しい
ワンポイント解説「2.平行平板コンデンサの静電容量$\ C \ $」の通り，コンデンサの静電容量$\ C \ $は，

$$\begin{eqnarray} C &=&\frac {\varepsilon S}{d} \\[ 5pt ] \end{eqnarray}$$ であり，ワンポイント解説「1.電荷$\ Q \ $と静電容量$\ C \ $及び電圧$\ V \ $の関係」の通り，蓄えられる電荷$\ Q \ $は，
$$\begin{eqnarray} Q &=&CV \\[ 5pt ] &=&\frac {\varepsilon S}{d}\cdot V \\[ 5pt ] \end{eqnarray}$$ となるため，誘電率$\ \varepsilon \ $が大きいほど，蓄えられる電荷量$\ Q \ $は大きくなります。

(3)：誤り
ワンポイント解説「3.平行平板コンデンサの電界$\ E \ $と電圧$\ V \ $の関係」の通り，極板間の電界$\ E \ $は，

$$\begin{eqnarray} E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}$$ となるため，誘電率$\ \varepsilon \ $に関係なく一定となります。

(4)：正しい
電荷$\ Q \ $から出る電束は$\ Q \ $であるため，単位面積当たりの電荷量の大きさは，電束密度（単位面積当たりの電束）に等しくなります。（ガウスの法則）

(5)：正しい
ワンポイント解説「5.平行平板コンデンサの静電エネルギー$\ W \ $」の通り，平行板コンデンサの静電エネルギー$\ W \ $は，

$$\begin{eqnarray} W &=&\frac {1}{2}CV^{2} \\[ 5pt ] &=&\frac {1}{2}\frac {\varepsilon S}{d}\cdot V^{2} \\[ 5pt ] \end{eqnarray}$$ となり，電極板の面積$\ S \ $を大きくすると増大します。