《理論》〈電磁気〉[H29:問17]エアギャップを含む磁気回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

巻数\( \ N \ \)のコイルを巻いた鉄心\( \ 1 \ \)と，空隙(エアギャップ)を隔てて置かれた鉄心\( \ 2 \ \)からなる図1のような磁気回路がある。この二つの鉄心の比透磁率はそれぞれ\( \ \mu _{\mathrm {r1}}=2000 \ \)，\( \ \mu _{\mathrm {r2}}=1000 \ \)であり，それらの磁路の平均の長さはそれぞれ\( \ l_{1}=200 \ \mathrm {mm} \ \)，\( \ l_{2}=98 \ \mathrm {mm} \ \)，空隙長は\( \ \delta =1 \ \mathrm {mm} \ \)である。ただし，鉄心\( \ 1 \ \)及び鉄心\( \ 2 \ \)のいずれの断面も同じ形状とし，磁束は断面内で一様で，漏れ磁束や空隙における磁束の広がりはないものとする。このとき，次の(a)及び(b)の問に答えよ。

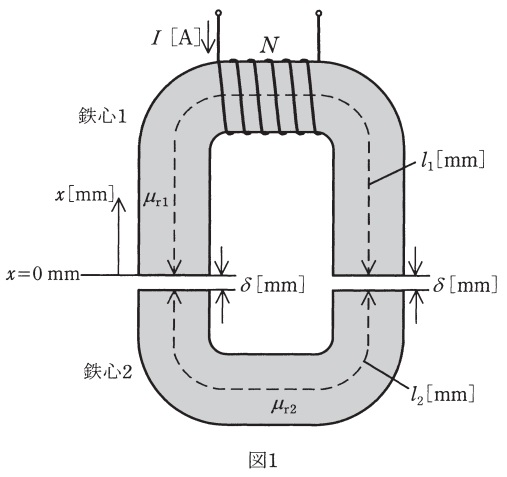
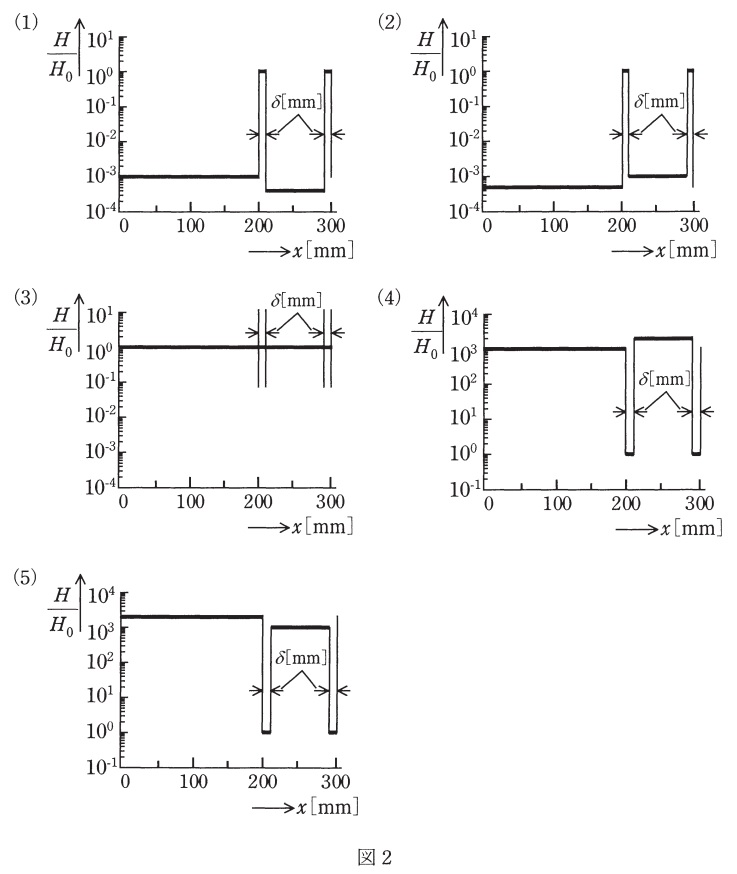
(a)　空隙における磁界の強さ\( \ H_{0} \ \)に対する磁路に沿った磁界の強さ\( \ H \ \)の比\( \ \displaystyle \frac {H}{H_{0}} \ \)を表すおおよその図として，最も近いものを図2の(1)～(5)のうちから一つ選べ。ただし，図1に示す\( \ x=0 \ \mathrm {mm} \ \)から時計回りに磁路を進む距離を\( \ x \ \mathrm {\left[ mm\right] } \ \)とする。また，図2は片対数グラフであり，空隙長\( \ \delta \ \mathrm {\left[ mm\right] } \ \)は実際より大きく表示している。

(b)　コイルに電流\( \ I=1 \ \mathrm {A} \ \)を流すとき，空隙における磁界の強さ\( \ H_{0} \ \)を\( \ 2\times 10^{4} \ \mathrm {A/m} \ \)以上とするのに必要なコイルの最小巻数\( \ N \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(24\)　　(2)　\(44\)　　(3)　\(240\)　　(4)　\(4400\)　　(5)　\(40400\)

【ワンポイント解説】

磁気回路は電気回路とは異なり，それほど複雑な回路計算を要求しません。最初はとっつきにくい面もありますが，公式を理解し問題に慣れてしまえば確実に得点源となりますので，本問をしっかりと理解しておきましょう。

1.アンペアの周回積分の法則
環状ソレノイド内部において，コイルの巻数\( \ N \ \)，電流\( \ I \ \)，磁路の平均長\( \ l \ \)のとき，磁界の強さ\( \ H \ \)とすると，
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ] \end{eqnarray}
\] となります。

2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係
図1において，真空の透磁率\( \ \mu _{0} \ \)，鉄心\( \ 1 \ \)，\( \ 2 \ \)の比透磁率\( \ \mu _{\mathrm {r1}} \ \)，\( \ \mu _{\mathrm {r2}} \ \)，真空中の磁界の強さ\( \ H_{0} \ \)，鉄心\( \ 1 \ \)，\( \ 2 \ \)中の磁界の強さ\( \ H_{1} \ \)，\( \ H_{2} \ \)とした時，
\[
\begin{eqnarray}
B&=&\mu _{0}H_{0} \\[ 5pt ] &=&\mu _{\mathrm {r1}}\mu _{0}H_{1} \\[ 5pt ] &=&\mu _{\mathrm {r2}}\mu _{0}H_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(2)
鉄心1，2中の磁界の強さ\( \ H_{1} \ \)，\( \ H_{2} \ \)とした時，ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係」より，
\[
\begin{eqnarray}
B&=&\mu _{0}H_{0}&=&\mu _{\mathrm {r1}}\mu _{0}H_{1}&=&\mu _{\mathrm {r2}}\mu _{0}H_{2} \\[ 5pt ] \end{eqnarray}
\] であり，各辺を\( \ \mu _{0} \ \)で割ると，
\[
\begin{eqnarray}
H_{0}&=&\mu _{\mathrm {r1}}H_{1}&=&\mu _{\mathrm {r2}}H_{2} \\[ 5pt ] \end{eqnarray}
\] となるため，これを整理すると，（→計算方法詳細）
\[
\begin{eqnarray}
\frac {H_{1}}{H_{0}}&=&\frac {1}{\mu _{\mathrm {r1}}} \\[ 5pt ] &=&\frac {1}{2000} \\[ 5pt ] \frac {H_{2}}{H_{0}}&=&\frac {1}{\mu _{\mathrm {r2}}} \\[ 5pt ] &=&\frac {1}{1000} \\[ 5pt ] \end{eqnarray}
\] となる。よって，上式を満たすグラフは(2)となる。

(b)解答：(2)
題意より，\( \ H_{0}=20000 \ \mathrm {[A/m]} \ \)とすると，
\[
\begin{eqnarray}
H_{1}&=&\frac {1}{\mu _{\mathrm {r1}}}H_{0} \\[ 5pt ] &=&\frac {1}{2000}\times 20000 \\[ 5pt ] &=&10 \ \mathrm {[A/m]} \\[ 5pt ] H_{2}&=&\frac {1}{\mu _{\mathrm {r2}}}H_{0} \\[ 5pt ] &=&\frac {1}{1000}\times 20000 \\[ 5pt ] &=&20 \ \mathrm {[A/m]} \\[ 5pt ] \end{eqnarray}
\] となる。アンペアの周回積分の法則より，
\[
\begin{eqnarray}
NI&=&H_{1}l_{1}+H_{2}l_{2}+2H_{0}\delta \\[ 5pt ] \end{eqnarray}
\] であるから，これに，\( \ I=1 \ \mathrm {A} \ \)，\( \ H_{1}=10 \ \mathrm {A/m} \ \)，\( \ H_{2}=20 \ \mathrm {A/m} \ \)，\( \ l_{1}=200 \ \mathrm {mm} \ \)，\( \ l_{2}=98 \ \mathrm {mm} \ \)，\( \ \delta =1 \ \mathrm {mm} \ \)を代入すると，
\[
\begin{eqnarray}
N\times 1&=&10\times 200\times 10^{-3}+20\times 98\times 10^{-3}+2\times 20000\times 1\times 10^{-3} \\[ 5pt ] N&=&2+1.96+40 \\[ 5pt ] &=&43.96　→　44 \\[ 5pt ] \end{eqnarray}
\] と求められる。