《理論》〈電気及び電子計測〉[R05上:問14]二電力計法を用いた電力の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

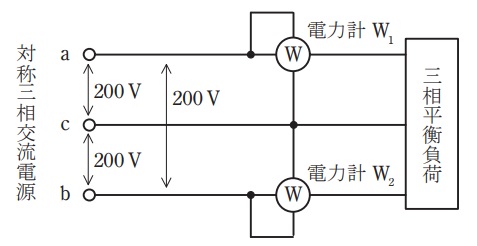
図のように，線間電圧\( \ 200 \ \mathrm {V} \ \)の対称三相交流電源から三相平衡負荷に供給する電力を二電力計法で測定する。\( \ 2 \ \)台の電力計\( \ \mathrm {W_{1}} \ \)及び\( \ \mathrm {W_{2}} \ \)を正しく接続したところ，電力計\( \ \mathrm {W_{2}} \ \)の指針が逆振れを起こした。電力計\( \ \mathrm {W_{2}} \ \)の電圧端子の極性を反転して接続した後，\( \ 2 \ \)台の電力計の指示値は，電力計\( \ \mathrm {W_{1}} \ \)が\( \ 490 \ \mathrm {W} \ \)，電力計\( \ \mathrm {W_{2}} \ \)が\( \ 25 \ \mathrm {W} \ \)であった。このときの対称三相交流電源が三相平衡負荷に供給する電力の値\( \ \mathrm {[W]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，三相交流電源の相回転は\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の順とし，電力計の電力損失は無視できるものとする。

　(1)　\( \ 25 \ \)　　(2)　\( \ 258 \ \)　　(3)　\( \ 465 \ \)　　(4)　\( \ 490 \ \)　　(5)　\( \ 515 \ \)

【ワンポイント解説】

二電力計法を用いた電力測定に関する問題です。
解法はそれほど難解ではありませんが，途中の逆振れの記述の意味をきちんと理解できるかが問われる問題であったかなと思います。
平成15年問13からの再出題となりますので，過去問研究をされていた方が圧倒的に有利な問題でした。

1.二電力計法
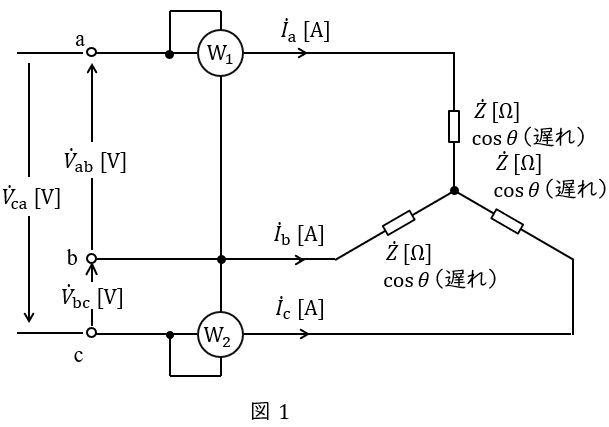
図1のように単相電力計を\( \ 2 \ \)個接続し，三相電力を測定する方法です。
電力計\( \ \mathrm {W}_{\mathrm {1}} \ \)は\( \ V_{\mathrm {ab}} \ \)と\( \ I_{\mathrm {a}} \ \)により電力を測定し，電力計\( \ \mathrm {W}_{\mathrm {2}} \ \)は\( \ V_{\mathrm {cb}} \ \)と\( \ I_{\mathrm {c}} \ \)により電力を測定します。
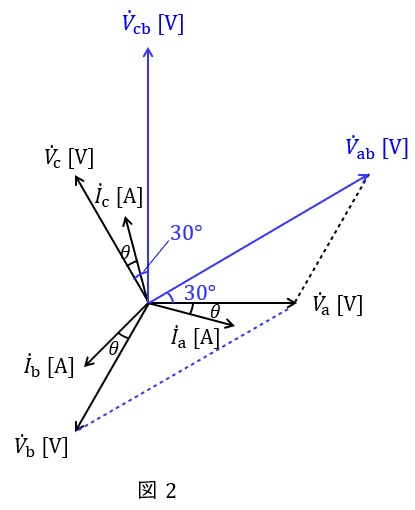
\( \ {\dot V}_{\mathrm {ab}}={\dot V}_{\mathrm {a}}-{\dot V}_{\mathrm {b}} \ \)と\( \ {\dot V}_{\mathrm {cb}}={\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {b}} \ \)はベクトル図で表すと図2のようになるため，\( \ {\dot V}_{\mathrm {ab}} \ \)と\( \ {\dot I}_{\mathrm {a}} \ \)の位相差は\( \ 30°+\theta \ \)，\( \ {\dot V}_{\mathrm {cb}} \ \)と\( \ {\dot I}_{\mathrm {c}} \ \)の位相差は\( \ 30°-\theta \ \)となります。
したがって，二つの電力計\( \ \mathrm {W}_{\mathrm {1}} \ \)及び\( \ \mathrm {W}_{\mathrm {2}} \ \)が求める電力\( \ P_{\mathrm {1}} \ \)及び\( \ P_{\mathrm {2}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&V_{\mathrm {ab}}I_{\mathrm {a}}\cos \left( 30°+\theta \right) \\[ 5pt ] P_{\mathrm {2}}&=&V_{\mathrm {cb}}I_{\mathrm {c}}\cos \left( 30°-\theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。加法定理により，上式を整理すると，
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&V_{\mathrm {ab}}I_{\mathrm {a}}\left( \cos 30° \cos \theta – \sin 30° \sin \theta \right) \\[ 5pt ] &=&V_{\mathrm {ab}}I_{\mathrm {a}}\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) \\[ 5pt ] P_{\mathrm {2}}&=&V_{\mathrm {cb}}I_{\mathrm {c}}\left( \cos 30° \cos \theta + \sin 30° \sin \theta \right) \\[ 5pt ] &=&V_{\mathrm {cb}}I_{\mathrm {c}}\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] となり，三相平衡回路である場合\( \ V_{\mathrm {ab}}=V_{\mathrm {cb}}=V \ \)，\( \ I_{\mathrm {a}}=I_{\mathrm {c}}=I \ \)とおけるので，
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) \\[ 5pt ] P_{\mathrm {2}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。上式の第\( \ 1 \ \)式と第\( \ 2 \ \)式を加えると，
\[
\begin{eqnarray}
P_{\mathrm {1}}+P_{\mathrm {2}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) +VI\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) \\[ 5pt ] &=&\sqrt {3}VI\cos \theta \\[ 5pt ] \end{eqnarray}
\] となり，三相有効電力が求められます。また，両式の差をとると，
\[
\begin{eqnarray}
P_{\mathrm {2}}-P_{\mathrm {1}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) -VI\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) \\[ 5pt ] &=&VI\sin \theta \\[ 5pt ] \end{eqnarray}
\] となることから，差をとって\( \ \sqrt {3} \ \)倍すれば三相無効電力が求められます。

【解答】

解答：(3)
電力計\( \ \mathrm {W_{1}} \ \)が\( \ 490 \ \mathrm {W} \ \)，電力計\( \ \mathrm {W_{2}} \ \)が\( \ 25 \ \mathrm {W} \ \)であるが，電力計\( \ \mathrm {W_{2}} \ \)は極性を反転したため\( \ -25 \ \mathrm {W} \ \)と考えれば良い。よって，求める有効電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P&=&490-25 \\[ 5pt ] &=&465 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。