《理論》〈電気回路〉[R05下:問9]高調波を含むひずみ波交流による電力に関する計算問題

【問題】

【難易度】★★★★★（難しい）

次式に示す電圧$\ e \ \mathrm {[V]} \ $及び電流$\ i \ \mathrm {[A]} \ $による電力の値$\ \mathrm {[kW]} \ $として，最も近いものを次の(1)～(5)のうちから一つ選べ。
$$\begin{eqnarray} e&=&100\sin \omega t+50 \sin \left( 3\omega t-\frac {\pi }{6}\right) \ \mathrm {[V]} \\[ 5pt ] i&=&20\sin \left( \omega t-\frac {\pi }{6}\right) +10\sqrt {3} \sin \left( 3\omega t+\frac {\pi }{6}\right) \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$

　(1)　$\ 0.95 \ $　　(2)　$\ 1.08 \ $　　(3)　$\ 1.16 \ $　　(4)　$\ 1.29 \ $　　(5)　$\ 1.34 \ $　　

【ワンポイント解説】

高調波を含む交流の電力を求める問題です。
この内容を正確に理解するためにはフーリエ級数展開や積分を理解していなければなりません。電験対策としては数学的な理解は一旦置いておき，解き方を暗記するようにして下さい。
本問はやや古いですが平成8年問11からの再出題となります。

1.電圧・電流の瞬時値からの電力の導出
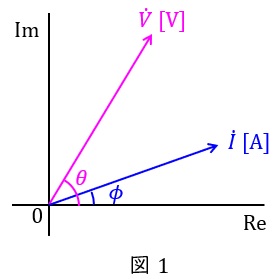
電圧及び電流の実効値が$\ V \ \mathrm {[V]} \ $及び$\ I \ \mathrm {[A]} \ $，角周波数が$\ \omega \ \mathrm {[rad / s]} \ $，電圧及び電流の初期位相が$\ \theta \ \mathrm {[rad]} \ $及び$\ \phi \ \mathrm {[rad]} \ $の正弦波交流があるとき，それぞれの瞬時値は，
$$\begin{eqnarray} v &=& \sqrt {2}V \sin \left( \omega t +\theta \right) \\[ 5pt ] i &=& \sqrt {2}I \sin \left( \omega t +\phi \right) \\[ 5pt ] \end{eqnarray}$$ となり，極座標平面では図1のように表されます。このとき，有効電力$\ P \ \mathrm {[W]} \ $は，
$$\begin{eqnarray} P &=&VI \cos \left( \theta -\phi \right) \\[ 5pt ] \end{eqnarray}$$ で求められます。

【解答】

解答：(2)
基本波と第$\ 3 \ $調波成分を分けて考えると，基本波成分による電力$\ P_{1} \ \mathrm {[kW]} \ $は，ワンポイント解説「1.電圧・電流の瞬時値からの電力の導出」の通り，
$$\begin{eqnarray} P_{1} &=&\frac {100}{\sqrt {2}}\times \frac {20}{\sqrt {2}} \cos \left\{ 0-\left( -\frac {\pi }{6}\right) \right\} \\[ 5pt ] &=&1 \ 000 \cos \frac {\pi }{6} \\[ 5pt ] &=&1 \ 000 \times \frac {\sqrt {3}}{2} \\[ 5pt ] &≒&866.0 \ \mathrm {[W]}　→　0.866 \ 0 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}$$ となり，第$\ 3 \ $調波成分による電力$\ P_{3} \ \mathrm {[kW]} \ $は，
$$\begin{eqnarray} P_{3} &=&\frac {50}{\sqrt {2}}\times \frac {10\sqrt {3}}{\sqrt {2}} \cos \left\{ \left( -\frac {\pi }{6}\right) -\frac {\pi }{6} \right\} \\[ 5pt ] &=&250\sqrt {3} \cos \left( -\frac {\pi }{3}\right) \\[ 5pt ] &=&250\sqrt {3} \times \frac {1}{2} \\[ 5pt ] &≒&216.5 \ \mathrm {[W]}　→　0.216 \ 5 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}$$ となる。したがって，合わせた電力$\ P \ \mathrm {[kW]} \ $は，
$$\begin{eqnarray} P &=&P_{1}+P_{3} \\[ 5pt ] &=&0.866 \ 0+0.216 \ 5 \\[ 5pt ] &≒&1.08 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}$$ と求められる。