Contents
【問題】
【難易度】★★★★☆(やや難しい)
図のように,起電力\( \ E \ \mathrm {[V]} \ \),内部抵抗\( \ r \ \mathrm {[\Omega ]} \ \)の電池\( \ n \ \)個と可変抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を直列に接続した回路がある。この回路において,可変抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費される電力が最大になるようにその値\( \ \mathrm {[\Omega ]} \ \)を調整した。このとき,回路に流れる電流\( \ I \ \)の値\( \ \mathrm {[A]} \ \)を表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
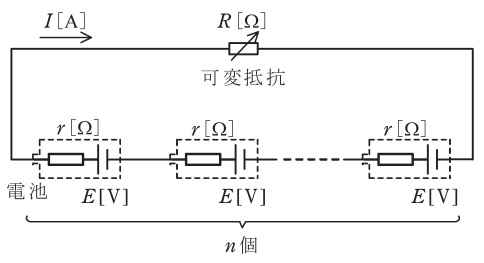
(1) \( \ \displaystyle \frac {E}{r} \ \) (2) \( \ \displaystyle \frac {nE}{\displaystyle \left( \frac {1}{n}+n \right) r} \ \) (3) \( \ \displaystyle \frac {nE}{ \left( 1+n \right) r} \ \)
(4) \( \ \displaystyle \frac {E}{2r} \ \) (5) \( \ \displaystyle \frac {nE}{2} \ \)
【ワンポイント解説】
可変抵抗で消費される電力が最大となるときの電流値を求める問題です。
最大電力の導出には微分積分の知識もしくは相加相乗という特殊な公式を利用して解く必要があるので,\( \ 3 \ \)種においては覚えておくことが重要となります。
1.可変抵抗で消費される最大電力
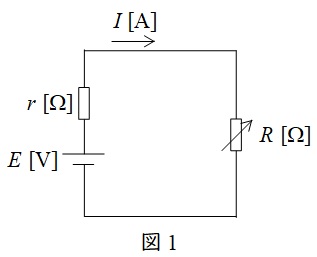
図1のように,電源\( \ E \ \mathrm {[V]} \ \)に抵抗\( \ r \ \mathrm {[\Omega ]} \ \)と可変抵抗\( \ R \ \mathrm {[\Omega ]} \ \)が接続されているときの,可変抵抗\( \ R \ \)で消費される最大電力を考えます。
図1の回路に流れる電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {E}{R+r} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ R \ \)で消費される電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P&=&RI^{2} \\[ 5pt ]
&=&R\left( \frac {E}{R+r}\right) ^{2} \\[ 5pt ]
&=&\frac {RE^{2}}{R^{2}+2rR+r^{2}} \\[ 5pt ]
&=&\frac {E^{2}}{\displaystyle R+2r+\frac {r^{2}}{R}} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ P \ \)が最大となるのは,上式の分母\( \ f\left( R \right) =\displaystyle R+2r+\frac {r^{2}}{R} \ \)が最小となるときなので,\( \ f\left( R \right) \ \)を微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}f}{\mathrm {d}R}&=&1-\frac {r^{2}}{R^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}f }{\mathrm {d}R} \ \)が零となるとき,\( \ f\left( R \right) \ \)が最小となるので,
\[
\begin{eqnarray}
1-\frac {r^{2}}{R^{2}}&=&0 \\[ 5pt ]
1&=&\frac {r^{2}}{R^{2}} \\[ 5pt ]
R^{2}&=&r^{2} \\[ 5pt ]
R&=&r \\[ 5pt ]
\end{eqnarray}
\]
の条件を満たすとき,\( \ P \ \)は最大となり,その値\( \ P_{\mathrm {m}} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {m}}&=&\frac {E^{2}}{\displaystyle r+2r+\frac {r^{2}}{r}} \\[ 5pt ]
&=&\frac {E^{2}}{4r} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
解答:(4)
回路は電池\( \ n \ \)個が直列に接続されているので,回路を変形すると図2のようになる。
ワンポイント解説「1.可変抵抗で消費される最大電力」の通り,可変抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費される電力が最大となるのは,\( \ nr=R \ \)のときであるから,そのときの電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {nE}{R+nr} \\[ 5pt ]
&=&\frac {nE}{nr+nr} \\[ 5pt ]
&=&\frac {nE}{2nr} \\[ 5pt ]
&=&\frac {E}{2r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは