《理論》〈電気回路〉[R06上:問6]３つの電源と抵抗を直並列した回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図の回路において，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)には電流\( \ 0.3 \ \mathrm {A} \ \)が流れている。抵抗\( \ R \ \)の値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

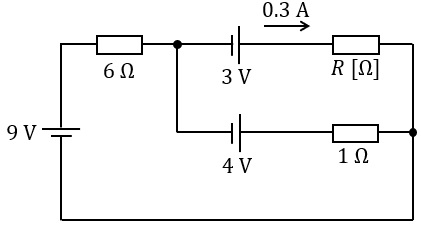
　(1)　\( \ 2.0 \ \)　　(2)　\( \ 2.8 \ \)　　(3)　\( \ 3.7 \ \)　　(4)　\( \ 4.9 \ \)　　(5)　\( \ 25 \ \)

【ワンポイント解説】

\( \ 3 \ \)つの電源と抵抗を直並列した回路の問題です。
様々な解き方が想定されますが，この問題の場合には単純にキルヒホッフの法則を使用しても解けます。
知識が増えてくると発生してしまう罠ですが，あくまで最初はキルヒホッフの法則で問題なく解けるかを考えてから他の方法を検討してみると良いかと思います。

1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが，法則を説明できる必要はなく，計算で使いこなせることが重要です。
①第1法則（電流則）
　回路の接続点に流入する電流の和と流出する電流の和が等しい。

　図1で言えば，例えば接続点\( \ \mathrm {A} \ \)において，
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ] \end{eqnarray}
\] 　となります。

②第2法則（電圧則）
　任意の閉回路において，起電力の総和と抵抗の電圧降下の和は等しい。

　図1で言えば，例えば閉回路\( \ 1 \ \)において，
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ] \end{eqnarray}
\] 　となります。

【解答】

解答：(1)
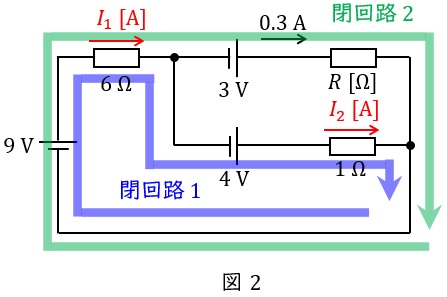
図2に示すように\( \ 6 \ \mathrm {\Omega } \ \)の抵抗に流れる電流を\( \ I_{1} \ \mathrm {[A]} \ \)，\( \ 1 \ \mathrm {\Omega } \ \)の抵抗に流れる電流を\( \ I_{2} \ \mathrm {[A]} \ \)とする。
キルヒホッフの法則の電流則より，
\[
\begin{eqnarray}
I_{1} &=&I_{2}+0.3　・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となり，閉回路\( \ 1 \ \)にキルヒホッフの法則の電圧則を適用すると，
\[
\begin{eqnarray}
9+4 &=&6\times I_{1}+1\times I_{2} \\[ 5pt ] 6I_{1}+I_{2} &=&13　・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となるので，①を②に代入すれば，
\[
\begin{eqnarray}
6\left( I_{2}+0.3\right) +I_{2} &=&13 \\[ 5pt ] 6I_{2}+1.8+I_{2} &=&13 \\[ 5pt ] 7I_{2} &=&11.2 \\[ 5pt ] I_{2} &=&1.6 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。これを①に代入すれば，
\[
\begin{eqnarray}
I_{1} &=&1.6+0.3 \\[ 5pt ] &=&1.9 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，閉回路\( \ 2 \ \)にキルヒホッフの法則の電圧則を適用すると，
\[
\begin{eqnarray}
9+3 &=&6\times I_{1}+R\times 0.3 \\[ 5pt ] 12 &=&6\times 1.9+0.3R \\[ 5pt ] 0.3R &=&0.6 \\[ 5pt ] R &=&2.0 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。