《理論》〈電気回路〉[H25:問15]三相交流回路の消費電力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

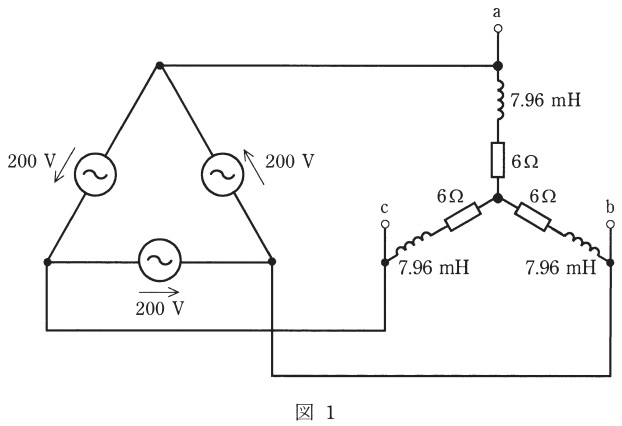
図1のように，周波数\( \ 50 \ \mathrm {[Hz]} \ \)，電圧\( \ 200 \ \mathrm {[V]} \ \)の対称三相交流電源に，インダクタンス\( \ 7.96 \ \mathrm {[mH]} \ \)のコイルと\( \ 6 \ \mathrm {[\Omega ]} \ \)の抵抗からなる平衡三相負荷を接続した交流回路がある。次の(a)及び(b)の問に答えよ。

(a)　図1において，三相負荷が消費する有効電力\( \ P \ \mathrm {[W]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(1890\)　　(2)　\(3280\)　　(3)　\(4020\)　　(4)　\(5680\)　　(5)　\(9840\)

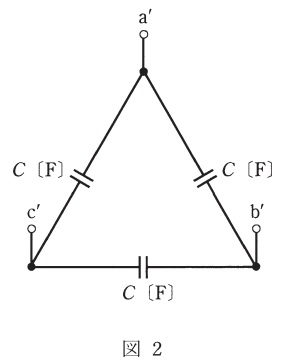
(b)　図2のように，静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサを\( \ \Delta \ \)結線し，その端子\( \ \mathrm {a}^{\prime } \ \),\( \ \mathrm {b}^{\prime } \ \)及び\( \ \mathrm {c}^{\prime } \ \)をそれぞれ図1の端子\( \ \mathrm {a} \ \),\( \ \mathrm {b} \ \)及び\( \ \mathrm {c} \ \)に接続した。その結果，三相交流電源からみた負荷の力率が\( \ 1 \ \)になった。静電容量\( \ C \ \mathrm {[F]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(6.28\times 10^{-5}\)　　(2)　\(8.88\times 10^{-5}\)　　(3)　\(1.08\times 10^{-4}\)
　(4)　\(1.26\times 10^{-4}\)　　(5)　\(1.88\times 10^{-4}\)

【ワンポイント解説】

三相交流回路の問題は毎年のように\( \ \mathrm {B} \ \)問題で出題され，計算も多く苦戦する受験生が多い分野です。比較的パターン化されているところもあるので，過去問学習を繰り返すことが大事であると思います。

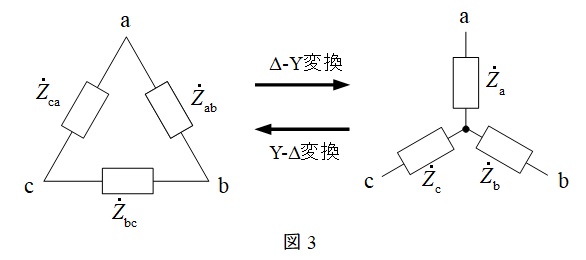
1.\(\Delta -\mathrm {Y}\)変換と\(\mathrm {Y}-\Delta \)変換
①\(\Delta -\mathrm {Y}\)変換
図3において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\(\mathrm {Y}-\Delta \)変換
図3において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\] となります。

【関連する「電気の神髄」記事】

　　Y⇔Δ回路のインピーダンス変換式

【解答】

(a)解答：(4)
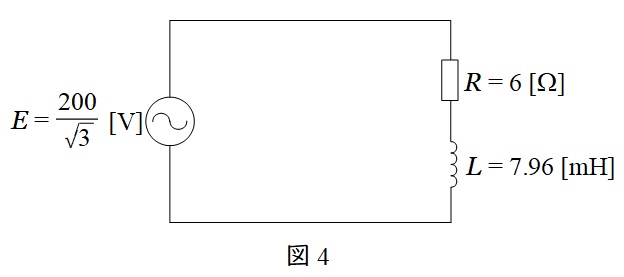
図1において，三相電源の相電圧の大きさ\( \ E \ \)は\( \ \displaystyle \frac {200}{\sqrt {3}} \ \mathrm {V} \ \)であり，三相対称回路であるから，一相分の等価回路は図4のようになる。
図4において，回路のインピーダンス\( \ Z \ \)の大きさは，
\[
\begin{eqnarray}
Z &=&\sqrt {R^{2}+\left( 2\pi f L \right) ^{2}} \\[ 5pt ] &=&\sqrt {6^{2}+\left( 2\pi \times 50 \times 7.96\times 10^{-3} \right) ^{2}} \\[ 5pt ] &≒&6.500 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，回路を流れる電流\( \ I \ \)の大きさは，
\[
\begin{eqnarray}
I &=&\frac {E}{Z} \\[ 5pt ] &=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{6.500} \\[ 5pt ] &≒&17.76 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，三相負荷が消費する有効電力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&3RI^{2} \\[ 5pt ] &=&3\times 6\times 17.76^{2} \\[ 5pt ] &≒&5678　→　5680 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
図2の静電容量\( \ C \ \mathrm {[F]} \ \)を\(\Delta -\mathrm {Y}\)変換すると，
\[
\begin{eqnarray}
\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}\cdot \frac {1}{\mathrm {j}\omega C}}{\displaystyle \frac {1}{\mathrm {j}\omega C}+\frac {1}{\mathrm {j}\omega C}+\frac {1}{\mathrm {j}\omega C}}&=&\frac {1}{\mathrm {j}3\omega C} \\[ 5pt ] \end{eqnarray}
\] となるので，一相分の等価回路は図5の通りとなる。

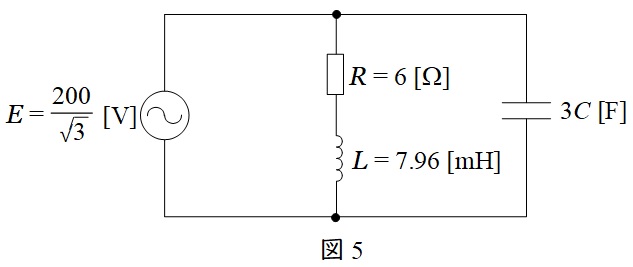
図5において，回路の並列合成アドミタンス\( \ \dot Y \ \)は，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R+\mathrm {j}\omega L}+\mathrm {j}3\omega C \\[ 5pt ] &=&\frac {1+\mathrm {j}3\omega C\left( R+\mathrm {j}\omega L\right) }{R+\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1-3\omega ^{2}LC+\mathrm {j}3\omega CR}{R+\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1-3\omega ^{2}LC+\mathrm {j}3\omega CR }{R+\mathrm {j}\omega L}\times \frac {R-\mathrm {j}\omega L}{R-\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {\left( 1-3\omega ^{2}LC+\mathrm {j}3\omega CR\right) \left( R-\mathrm {j}\omega L\right) }{R^{2}+\left( \omega L\right) ^{2}} \\[ 5pt ] &=&\frac {R\left( 1-3\omega ^{2}LC\right) +\mathrm {j}3\omega CR^{2}-\mathrm {j}\omega L\left( 1-3\omega ^{2}LC\right) + 3\omega ^{2}LCR }{R^{2}+\left( \omega L\right) ^{2}} \\[ 5pt ] &=&\frac {R\left( 1-3\omega ^{2}LC\right) + 3\omega ^{2}LCR +\mathrm {j}\left[ 3\omega CR^{2}-\omega L\left( 1-3\omega ^{2}LC\right) \right] }{R^{2}+\left( \omega L\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となる。力率が\( \ 1 \ \)であるためには，\( \ \dot Y \ \)の虚部が零でなければならないので，
\[
\begin{eqnarray}
3\omega CR^{2}-\omega L\left( 1-3\omega ^{2}LC\right) &=&0 \\[ 5pt ] 3\omega CR^{2}&=&\omega L\left( 1-3\omega ^{2}LC\right) \\[ 5pt ] 3CR^{2}&=&L\left( 1-3\omega ^{2}LC\right) \\[ 5pt ] 3R^{2}C+3\omega ^{2}L^{2}C&=&L \\[ 5pt ] C&=&\frac {L}{3R^{2}+3\omega ^{2}L^{2}} \\[ 5pt ] \end{eqnarray}
\] となり，各値を代入すると，
\[
\begin{eqnarray}
C&=&\frac {7.96\times 10^{-3}}{3\times 6^{2}+3\times \left( 2\pi \times 50\right) ^{2}\left( 7.96\times 10^{-3}\right) ^{2}} \\[ 5pt ] &≒&0.0000628　→　6.28 \times 10^{-5} \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] と求められる。