Contents
【問題】
【難易度】★★★★★(難しい)
次式に示す電圧\( \ e \ \mathrm {[V]} \ \)及び電流\( \ i \ \mathrm {[A]} \ \)による電力の値\( \ \mathrm {[kW]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{eqnarray}
e&=&100\sin \omega t+50 \sin \left( 3\omega t-\frac {\pi }{6}\right) \ \mathrm {[V]} \\[ 5pt ]
i&=&20\sin \left( \omega t-\frac {\pi }{6}\right) +10\sqrt {3} \sin \left( 3\omega t+\frac {\pi }{6}\right) \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
(1) \( \ 0.95 \ \) (2) \( \ 1.08 \ \) (3) \( \ 1.16 \ \) (4) \( \ 1.29 \ \) (5) \( \ 1.34 \ \)
【ワンポイント解説】
高調波を含む交流の電力を求める問題です。
この内容を正確に理解するためにはフーリエ級数展開や積分を理解していなければなりません。電験対策としては数学的な理解は一旦置いておき,解き方を暗記するようにして下さい。
本問は令和5年下期問9及び平成8年問11からの再出題となります。直近の過去問からの再出題はこれまでの電験にはなかった新傾向となります。
1.電圧・電流の瞬時値からの電力の導出
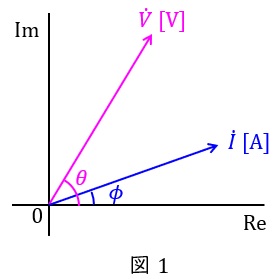
電圧及び電流の実効値が\( \ V \ \mathrm {[V]} \ \)及び\( \ I \ \mathrm {[A]} \ \),角周波数が\( \ \omega \ \mathrm {[rad / s]} \ \),電圧及び電流の初期位相が\( \ \theta \ \mathrm {[rad]} \ \)及び\( \ \phi \ \mathrm {[rad]} \ \)の正弦波交流があるとき,それぞれの瞬時値は,
\[
\begin{eqnarray}
v &=& \sqrt {2}V \sin \left( \omega t +\theta \right) \\[ 5pt ]
i &=& \sqrt {2}I \sin \left( \omega t +\phi \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,極座標平面では図1のように表されます。このとき,有効電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&VI \cos \left( \theta -\phi \right) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
解答:(2)
基本波と第\( \ 3 \ \)調波成分を分けて考えると,基本波成分による電力\( \ P_{1} \ \mathrm {[kW]} \ \)は,ワンポイント解説「1.電圧・電流の瞬時値からの電力の導出」の通り,
\[
\begin{eqnarray}
P_{1} &=&\frac {100}{\sqrt {2}}\times \frac {20}{\sqrt {2}} \cos \left\{ 0-\left( -\frac {\pi }{6}\right) \right\} \\[ 5pt ]
&=&1 \ 000 \cos \frac {\pi }{6} \\[ 5pt ]
&=&1 \ 000 \times \frac {\sqrt {3}}{2} \\[ 5pt ]
&≒&866.0 \ \mathrm {[W]} → 0.866 \ 0 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となり,第\( \ 3 \ \)調波成分による電力\( \ P_{3} \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P_{3} &=&\frac {50}{\sqrt {2}}\times \frac {10\sqrt {3}}{\sqrt {2}} \cos \left\{ \left( -\frac {\pi }{6}\right) -\frac {\pi }{6} \right\} \\[ 5pt ]
&=&250\sqrt {3} \cos \left( -\frac {\pi }{3}\right) \\[ 5pt ]
&=&250\sqrt {3} \times \frac {1}{2} \\[ 5pt ]
&≒&216.5 \ \mathrm {[W]} → 0.216 \ 5 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,合わせた電力\( \ P \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P &=&P_{1}+P_{3} \\[ 5pt ]
&=&0.866 \ 0+0.216 \ 5 \\[ 5pt ]
&≒&1.08 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは