《理論》〈電気回路〉[R06下:問10]RC回路の過渡状態と定常状態の時に流れる電流の比に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図に示す回路において，スイッチ\( \ \mathrm {S} \ \)を閉じた瞬間（時刻\( \ t=0 \ \)）に点\( \ \mathrm {A} \ \)を流れる電流を\( \ I_{0} \ \mathrm {[A]} \ \)とし，十分に時間が経ち，定常状態に達したのちに点\( \ \mathrm {A} \ \)を流れる電流を\( \ I \ \mathrm {[A]} \ \)とする。電流比\( \ \displaystyle \frac {I_{0}}{I} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，コンデンサの初期電荷は零とする。

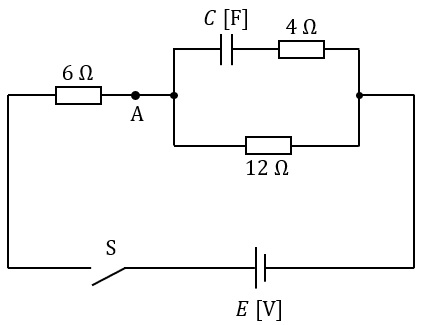
　(1)　\( \ 0.5 \ \)　　(2)　\( \ 1.0 \ \)　　(3)　\( \ 1.5 \ \)　　(4)　\( \ 2.0 \ \)　　(5)　\( \ 2.5 \ \)

【ワンポイント解説】

\( \ RC \ \)直並列回路の過渡状態と定常状態における電流比を考える問題です。
解説ではきちんと\( \ I_{0} \ \mathrm {[A]} \ \)と\( \ I \ \mathrm {[A]} \ \)を求めていますが，電圧が同じ場合抵抗比と電流比が逆数の関係にあることを知っていれば合成抵抗を求めるだけで即座に解を求めることが可能となります。
本問は全く同じではありませんが，平成22年問10の類題となります。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので，電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに十分に電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

3.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
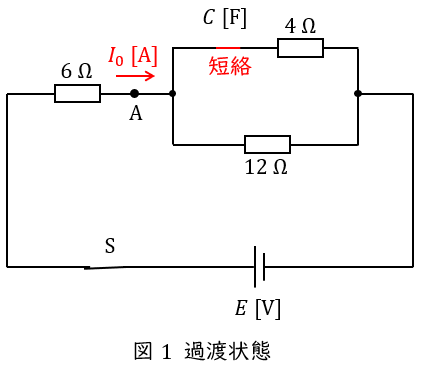
スイッチ\( \ \mathrm {S} \ \)を閉じた瞬間の回路図は，ワンポイント解説「2.過渡現象におけるコンデンサの過渡状態と定常状態」の通り，コンデンサは短絡と考えれば良いので，図1のようになる。
このとき，回路の合成抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「3.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{0}&=&6+\frac {4\times 12}{4+12} \\[ 5pt ] &=&9 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，点\( \ \mathrm {A} \ \)を流れる電流\( \ I_{0} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{0}&=&\frac {E}{R_{0}} \\[ 5pt ] &=&\frac {E}{9} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。

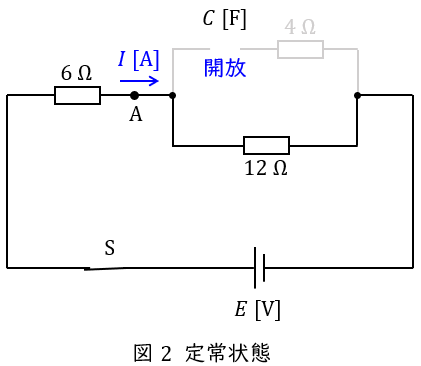
また，定常状態の時の回路図は，ワンポイント解説「2.過渡現象におけるコンデンサの過渡状態と定常状態」の通り，コンデンサは開放と考えれば良いので，図2のようになる。
このとき，回路の合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「3.合成抵抗」の通り，
\[
\begin{eqnarray}
R&=&6+12 \\[ 5pt ] &=&18 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，点\( \ \mathrm {A} \ \)を流れる電流\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I&=&\frac {E}{R} \\[ 5pt ] &=&\frac {E}{18} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。

よって，求める電流比\( \ \displaystyle \frac {I_{0}}{I} \ \)は，
\[
\begin{eqnarray}
\frac {I_{0}}{I}&=&\frac {\displaystyle \frac {E}{9}}{\displaystyle \frac {E}{18}} \\[ 5pt ] &=&\frac {E\times 18}{E\times 9} \\[ 5pt ] &=&2.0 \\[ 5pt ] \end{eqnarray}
\] と求められる。