《理論》〈電気及び電子計測〉[R06下:問16]ブリッジの平衡条件を利用した回路演算に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のブリッジ回路を用いて，未知抵抗\( \ R_{x} \ \)を測定したい。抵抗\( \ R_{1}=3 \ \mathrm {k\Omega } \ \)，\( \ R_{2}=2 \ \mathrm {k\Omega } \ \)，\( \ R_{4}=3 \ \mathrm {k\Omega } \ \)とし，\( \ R_{3}=6 \ \mathrm {k\Omega } \ \)の滑り抵抗器の接触子の接点\( \ \mathrm {C} \ \)をちょうど中央に調整したとき\( \ \left( R_{\mathrm {ac}}=R_{\mathrm {bc}}=3 \ \mathrm {k\Omega } \right) \ \)ブリッジが平衡したという。次の(a)及び(b)の問に答えよ。

ただし，直流電圧源は\( \ 6 \ \mathrm {V} \ \)とし，電流計の内部抵抗は無視できるものとする。

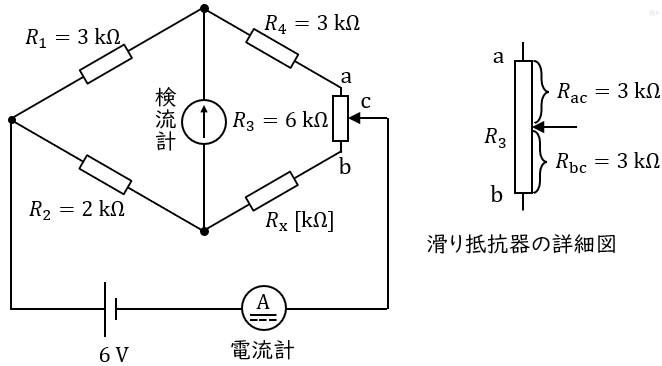
(a)　未知抵抗\( \ R_{x} \ \)の値\( \ \mathrm {[k\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.1 \ \)　　(2)　\( \ 0.5 \ \)　　(3)　\( \ 1.0 \ \)　　(4)　\( \ 1.5 \ \)　　(5)　\( \ 2.0 \ \)

(b)　平衡時の電流計の指示値\( \ \mathrm {[mA]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0 \ \)　　(2)　\( \ 0.4 \ \)　　(3)　\( \ 1.5 \ \)　　(4)　\( \ 1.7 \ \)　　(5)　\( \ 2.0 \ \)

【ワンポイント解説】

直流ブリッジの平衡条件を用いて未知の抵抗及び電流計の値を求める問題です。
解法はそれほど難解ではありませんが，(b)の設問で電流計の指示値を検流計の指示値と間違える受験生が多かったので注意して下さい。
本問は平成18年問16からの再出題となります。

1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.直流ブリッジの平衡条件
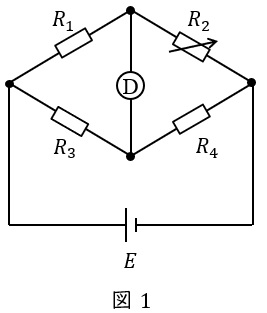
直流ブリッジ回路は抵抗の抵抗値を求める方法であり，ホイートストンブリッジと呼ばれます。
図1の回路において，検出器\( \ Ⓓ \ \)に電流が流れない条件を平衡条件と言い，
\[
\begin{eqnarray}
R_{1}R_{4} &=& R_{2}R_{3} \\[ 5pt ] \end{eqnarray}
\] の関係があります。したがって，３つの既知の抵抗があれば，残りの１つの抵抗値を求めることができます。

【解答】

(a)解答：(3)
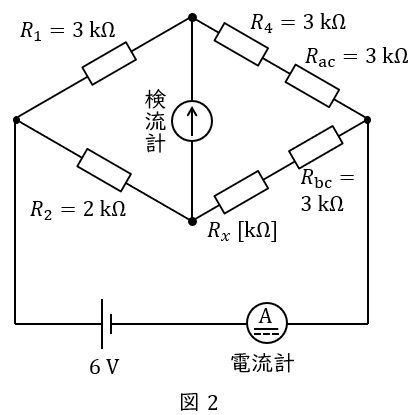
題意に沿ってブリッジが平衡したときの回路を描くと図2のようになる。
このときのブリッジの平衡条件は，ワンポイント解説「2.直流ブリッジの平衡条件」の通り，
\[
\begin{eqnarray}
R_{1}\left( R_{x}+R_{\mathrm {bc}}\right) &=& R_{2}\left( R_{4}+R_{\mathrm {ac}}\right) \\[ 5pt ] 3\times \left( R_{x}+3\right) &=& 2\times \left( 3+3\right) \\[ 5pt ] &=& 12 \\[ 5pt ] R_{x}+3 &=& 4 \\[ 5pt ] R_{x} &=& 1 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
ブリッジが平衡しているとき，検流計は切り離して考えても良いから，図2の回路の合成抵抗\( \ R \ \mathrm {[k\Omega ]} \ \)は，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R &=& \frac {\left( R_{1}+R_{4}+R_{\mathrm {ac}}\right) \left( R_{2}+R_{x}+R_{\mathrm {bc}}\right) }{\left( R_{1}+R_{4}+R_{\mathrm {ac}}\right) +\left( R_{2}+R_{x}+R_{\mathrm {bc}}\right) } \\[ 5pt ] &=& \frac {\left( 3+3+3\right) \left( 2+1+3\right) }{\left( 3+3+3\right) +\left( 2+1+3\right)} \\[ 5pt ] &=& \frac {54}{15} \\[ 5pt ] &=& 3.6 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，電流計に流れる電流の大きさ\( \ I \ \mathrm {[mA]} \ \)は，
\[
\begin{eqnarray}
I &=&\frac {6}{R} \\[ 5pt ] &=&\frac {6}{3.6\times 10^{3}} \\[ 5pt ] &≒& 1.67\times 10^{-3} \ \mathrm {[A]}　→　1.67 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。