Contents
【問題】
【難易度】★★★★☆(やや難しい)
図のように,\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサ,インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルからなる平衡三相負荷に線間電圧\( \ V \ \mathrm {[V]} \ \)の対称三相交流電源を接続した回路がある。次の(a)及び(b)の問に答えよ。
ただし,交流電源電圧の角周波数は\( \ \omega \ \mathrm {[rad / s]} \ \)とする。
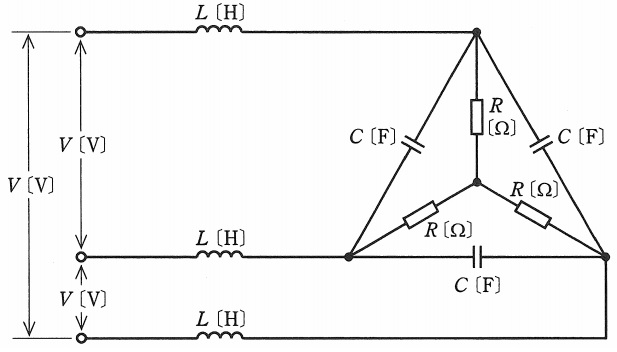
(a) 三相電源からみた平衡三相負荷の力率が\( \ 1 \ \)になったとき,インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルと静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサの関係を示す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ \displaystyle L=\frac {3C^{2}R^{2}}{1+9\left( \omega CR\right) ^{2}} \ \) (2) \( \ \displaystyle L=\frac {3CR^{2}}{1+9\left( \omega CR\right) ^{2}} \ \)
(3) \( \ \displaystyle L=\frac {3C^{2}R}{1+9\left( \omega CR\right) ^{2}} \ \) (4) \( \ \displaystyle L=\frac {9CR^{2}}{1+9\left( \omega CR\right) ^{2}} \ \)
(5) \( \ \displaystyle L=\frac {R}{1+9\left( \omega CR\right) ^{2}} \ \)
(b) 平衡三相負荷の力率が\( \ 1 \ \)になったとき,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサの端子電圧\( \ \mathrm {[V]} \ \)の値を示す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ \displaystyle \sqrt {3}V\sqrt {1+9\left( \omega CR\right) ^{2}} \ \) (2) \( \ \displaystyle V\sqrt {1+9\left( \omega CR\right) ^{2}} \ \)
(3) \( \ \displaystyle \frac {V\sqrt {1+9\left( \omega CR\right) ^{2}}}{\sqrt {3}} \ \) (4) \( \ \displaystyle \frac {\sqrt {3}V}{\sqrt {1+9\left( \omega CR\right) ^{2}}} \ \)
(5) \( \ \displaystyle \frac {V}{\sqrt {1+9\left( \omega CR\right) ^{2}}} \ \)
【ワンポイント解説】
\( \ \Delta -\mathrm {Y} \ \)変換を用いて演算を行うやや難易度が高めの問題です。
基本的に\( \ 3 \ \)種では平衡三相負荷が出題されるので,平衡三相負荷の\( \ \Delta -\mathrm {Y} \ \)変換及び一相分等価回路を描けるようにしておきましょう。
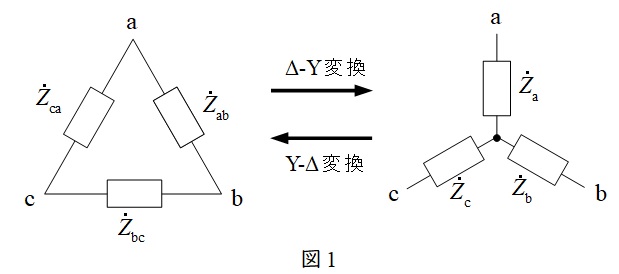
1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\]
となります。
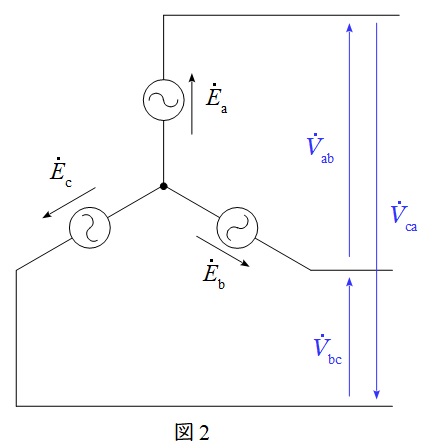
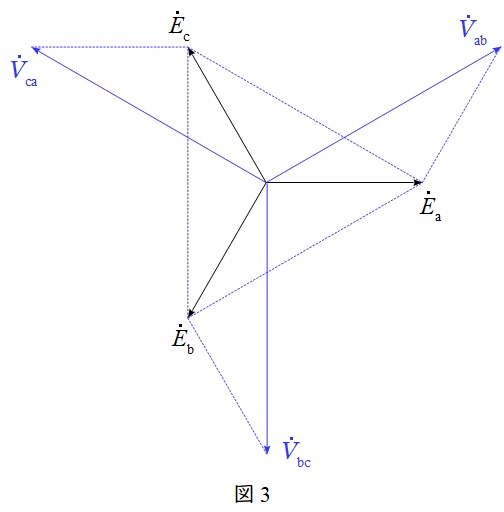
2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図2のような三相対称電源がある時,線間電圧と相電圧の関係は図3のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)進みであることが分かります。
【解答】
(a)解答:(2)
コンデンサ\( \ C \ \mathrm {[F]} \ \)を\( \ \Delta -\mathrm {Y} \ \)変換すると,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {Y}}&=&\frac {{\dot Z}_{\mathrm {\Delta }}}{3} \\[ 5pt ]
\frac {1}{\mathrm {j}\omega C_{\mathrm {Y}}}&=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{3} \\[ 5pt ]
&=& \frac {1}{\mathrm {j}3\omega C} \\[ 5pt ]
\frac {1}{C_{\mathrm {Y}}}&=& \frac {1}{3 C} \\[ 5pt ]
C_{\mathrm {Y}}&=& 3C \\[ 5pt ]
\end{eqnarray}
\]
となるので,問題図の回路は図4のように変換でき,さらに一相分等価回路は図5のようになる。
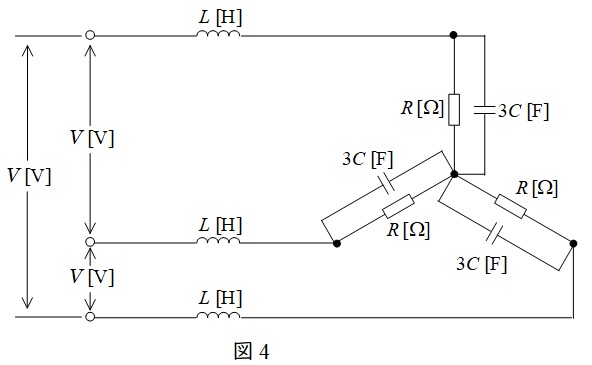
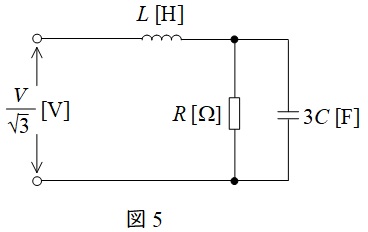
図5において,回路の合成インピーダンス\( \ \dot Z \ \)は,
\[
\begin{eqnarray}
\dot Z&=&\mathrm {j}\omega L+\frac {\displaystyle R\cdot \frac {1}{\mathrm {j}3\omega C}}{\displaystyle R+\frac {1}{\mathrm {j}3\omega C}} \\[ 5pt ]
&=&\mathrm {j}\omega L+\frac {\displaystyle \frac {R}{\mathrm {j}3\omega C}}{\displaystyle \frac {1+\mathrm {j}3\omega CR}{\mathrm {j}3\omega C}} \\[ 5pt ]
&=&\mathrm {j}\omega L+\frac {R}{1+\mathrm {j}3\omega CR} \\[ 5pt ]
&=&\mathrm {j}\omega L+\frac {R}{1+\mathrm {j}3\omega CR}\times \frac {1-\mathrm {j}3\omega CR}{1-\mathrm {j}3\omega CR} \\[ 5pt ]
&=&\mathrm {j}\omega L+\frac {R-\mathrm {j}3\omega CR^{2}}{1+9\left( \omega CR\right) ^{2}} \\[ 5pt ]
&=&\frac {R}{1+9\left( \omega CR\right) ^{2}}+\mathrm {j}\omega \left\{ L-\frac {3CR^{2}}{1+9\left( \omega CR\right) ^{2}} \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,力率が\( \ 1 \ \)となるためには,虚数部が零でなければならないので,
\[
\begin{eqnarray}
L-\frac {3CR^{2}}{1+9\left( \omega CR\right) ^{2}}&=&0 \\[ 5pt ]
L&=&\frac {3CR^{2}}{1+9\left( \omega CR\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(2)
図5のコンデンサ\( \ 3C \ \mathrm {[F]} \ \)にかかる電圧\( \ {\dot V}_{\mathrm {c}} \ \mathrm {[V]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {c}}&=&\frac {\displaystyle \frac {R-\mathrm {j}3\omega CR^{2}}{1+9\left( \omega CR\right) ^{2}}}{\dot Z}\cdot \frac {V}{\sqrt {3}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {R-\mathrm {j}3\omega CR^{2}}{1+9\left( \omega CR\right) ^{2}}}{\displaystyle \frac {R}{1+9\left( \omega CR\right) ^{2}}}\cdot \frac {V}{\sqrt {3}} \\[ 5pt ]
&=&\frac {R-\mathrm {j}3\omega CR^{2}}{R}\cdot \frac {V}{\sqrt {3}} \\[ 5pt ]
&=&\left( 1-\mathrm {j}3\omega CR\right)\cdot \frac {V}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ V_{\mathrm {c}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {c}}&=&\sqrt {1+9\left( \omega CR\right) ^{2}}\cdot \frac {V}{\sqrt {3}} \\[ 5pt ]
&=&\frac {V\sqrt {1+9\left( \omega CR\right) ^{2}}}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となる。コンデンサの端子電圧は線間電圧であるため,\( \ V_{\mathrm {c}} \ \mathrm {[V]} \ \)を\( \ \sqrt {3} \ \)倍すると,
\[
\begin{eqnarray}
\sqrt {3}V_{\mathrm {c}}&=&V\sqrt {1+9\left( \omega CR\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは