《理論》〈電磁気〉[R06下:問2]地球を導体球と見なしたときの静電容量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

地球を，真空中にある半径\( \ 6.37 \times 10^{6} \ \mathrm {m} \ \)の導体球と見なしたとき，地球の静電容量の値\( \ \mathrm {[F]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，真空の誘電率を\( \ \varepsilon _{0}=8.85\times 10^{-12} \ \mathrm {F/m} \ \)とする。

　(1)　\( \ 7.08\times 10^{-4} \ \)　　(2)　\( \ 4.45\times 10^{-3} \ \)　　(3)　\( \ 4.51\times 10^{3} \ \)　
　(4)　\( \ 5.67\times 10^{4} \ \)　　(5)　\( \ 1.78\times 10^{5} \ \)

【ワンポイント解説】

導体球の静電容量に関する問題です。
最初の取っ掛かりが迷うところですので，本問を通じて解法をマスターしておくようにして下さい。また，地球の大きさで考えた時の静電容量のオーダーがどの程度か本問で感覚を持っておくと良いでしょう。
本問は平成18年問1とほぼ同じ問題です。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.点電荷を置いたときの周囲の電位
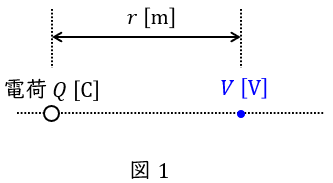
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)を置いた時，距離\( \ r \ \mathrm {[m]} \ \)離れた位置の電位\( \ V \ \mathrm {[V]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると，
\[
\begin{eqnarray}
V &=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ] \end{eqnarray}
\] となります。クーロンの法則\( \ \displaystyle F=\frac {Q_{1}Q_{2}}{4\pi \varepsilon _{0}r^{2}} \ \)や電界の式\( \ \displaystyle E=\frac {Q}{4\pi \varepsilon _{0}r^{2}} \ \)と似ているので合わせて覚えておきましょう。

【解答】

解答：(1)
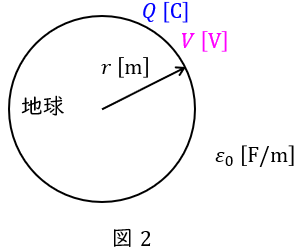
地球（導体球）に電荷\( \ Q \ \mathrm {[C]} \ \)を蓄えたときの地球（導体球）表面の電位\( \ V \ \mathrm {[V]} \ \)は，ワンポイント解説「2.点電荷を置いたときの周囲の電位」の通り，
\[
\begin{eqnarray}
V &=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ] \end{eqnarray}
\] となるので，静電容量\( \ C \ \mathrm {[F]} \ \)は，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
C &=&\frac {Q}{V} \\[ 5pt ] &=&\frac {Q}{\displaystyle \frac {Q}{4\pi \varepsilon _{0}r}} \\[ 5pt ] &=&4\pi \varepsilon _{0}r \\[ 5pt ] \end{eqnarray}
\] となる。したがって，各値を代入すると，
\[
\begin{eqnarray}
C &=&4\pi \varepsilon _{0}r \\[ 5pt ] &=&4\pi \times 8.85\times 10^{-12}\times 6.37\times 10^{6} \\[ 5pt ] &≒&7.08\times 10^{-4} \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] と求められる。