《理論》〈電気回路〉[R06下:問7]既知の抵抗と合成抵抗値から未知の抵抗の抵抗値の導出に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

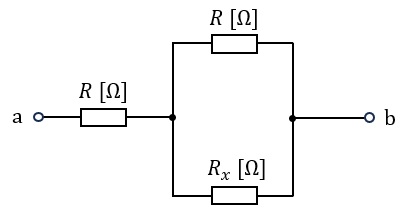
図の抵抗回路において，端子\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)間の合成抵抗\( \ R_{\mathrm {ab}} \ \)の値\( \ \mathrm {[\Omega ]} \ \)は\( \ 1.8R \ \mathrm {[\Omega ]} \ \)であった。このとき，抵抗\( \ R_{x} \ \)の値\( \ \mathrm {[\Omega ]} \ \)として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ R \ \)　　(2)　\( \ 2R \ \)　　(3)　\( \ 3R \ \)　　(4)　\( \ 4R \ \)　　(5)　\( \ 5R \ \)

【ワンポイント解説】

既知の抵抗\( \ R \ \)と合成抵抗値から未知の抵抗\( \ R_{x} \ \)を求める問題です。
合成抵抗の公式以外使用する必要がないため，正答率はかなり高くなると予想されます。しっかりと計算間違いせず得点できるようにしましょう。

1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
ワンポイント解説「1.合成抵抗」の通り，与えられている回路の合成抵抗を求める式より，
\[
\begin{eqnarray}
1.8R&=&R+\frac {RR_{x}}{R+R_{x}} \\[ 5pt ] \end{eqnarray}
\] の関係があるから，これを\( \ R_{x} \ \)について整理すると，
\[
\begin{eqnarray}
0.8R&=&\frac {RR_{x}}{R+R_{x}} \\[ 5pt ] 0.8R\left( R+R_{x}\right) &=&RR_{x} \\[ 5pt ] 0.8\left( R+R_{x}\right) &=&R_{x} \\[ 5pt ] 0.8R+0.8R_{x}&=&R_{x} \\[ 5pt ] 0.2R_{x}&=&0.8R \\[ 5pt ] R_{x}&=&4R \\[ 5pt ] \end{eqnarray}
\] と求められる。