《理論》〈電気及び電子計測〉[R07上:問16]電流電圧計の測定範囲拡大に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次に示す条件Ⅰ～Ⅲを満たす永久磁石可動コイル形電流電圧計を製作したい。永久磁石可動コイル形電流電圧計内部の接続の一部が図に示すようであるとき，次の(a)及び(b)の問に答えよ。ただし，コイルは内部抵抗\( \ r=5 \ \mathrm {\Omega } \ \)であり，最大\( \ 4 \ \mathrm {mA} \ \)まで直流電流を流すことができるものとする。

条件Ⅰ：切り替えスイッチを\( \ \mathrm {A} \ \)にしたときは，最大\( \ 1 \ \mathrm {A} \ \)の直流電流を測定できるものとする。

条件Ⅱ：切り替えスイッチを\( \ \mathrm {B} \ \)にしたときは，最大\( \ 100 \ \mathrm {mA} \ \)の直流電流を測定できるものとする。

条件Ⅲ：切り替えスイッチを\( \ \mathrm {C} \ \)にしたときは，最大\( \ 1.2 \ \mathrm {V} \ \)の直流電圧を測定できるものとする。

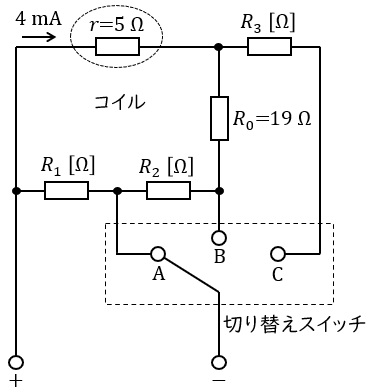
(a)　抵抗\( \ R_{1} \ \)の値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.1 \ \)　　(2)　\( \ 0.9 \ \)　　(3)　\( \ 4 \ \)　　(4)　\( \ 9.6 \ \)　　(5)　\( \ 9.96 \ \)

(b)　抵抗\( \ R_{3} \ \)の値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 2.36 \ \)　　(2)　\( \ 23.6 \ \)　　(3)　\( \ 25 \ \)　　(4)　\( \ 236 \ \)　　(5)　\( \ 2 \ 360 \ \)

【ワンポイント解説】

電流電圧計の測定範囲拡大に関する問題です。
スイッチを切り替えたとき，電流がどのように流れ，どの抵抗が分流器や倍率器になるかを理解することが重要です。
なお，分流器や倍率器の抵抗の大きさは公式として覚えても良いですが，分流の法則や分圧の法則を変形することで求められるので，必須の暗記事項ではありません。

1.分流器
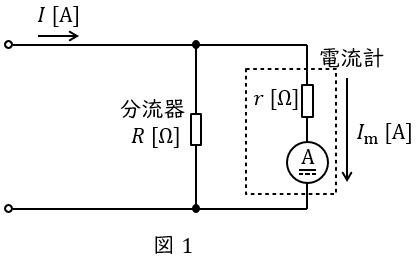
電流計に並列につなぐ抵抗器のことで，電流計の測定できる範囲を拡大することができるものです。図1のように電圧計の内部抵抗を\( \ r \ \mathrm {[\Omega ]} \ \)，分流器の抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)とすると，電流計に流れる電流\( \ I_{\mathrm {m}} \ \mathrm {[A]} \ \)は，分流の法則より，
\[
\begin{eqnarray}
I_{\mathrm {m}} &=&\frac {R}{R+r}I \\[ 5pt ] \end{eqnarray}
\] となり，倍率\( \ \displaystyle m=\frac {I}{I_{\mathrm {m}}} \ \)は，
\[
\begin{eqnarray}
m&=&\frac {I}{I_{\mathrm {m}}} \\[ 5pt ] &=&\frac {R+r}{R} \\[ 5pt ] &=&1+\frac {r}{R} \\[ 5pt ] \end{eqnarray}
\] となります。よって，分流器の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
m&=&1+\frac {r}{R} \\[ 5pt ] \frac {r}{R}&=&m-1 \\[ 5pt ] R&=&\frac {r}{m-1} \\[ 5pt ] \end{eqnarray}
\] と求められます。

2.倍率器
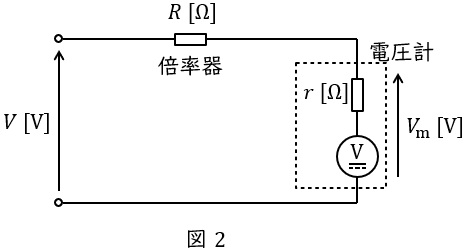
電圧計に直列につなぐ抵抗器のことで，電圧計の測定できる範囲を拡大することができるものです。図2のように電圧計の内部抵抗を\( \ r \ \mathrm {[\Omega ]} \ \)，倍率器の抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)とすると，電圧計に加わる電圧\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)は，分圧の法則より，
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&\frac {r}{R+r}V \\[ 5pt ] \end{eqnarray}
\] となり，倍率\( \ \displaystyle m=\frac {V}{V_{\mathrm {m}}} \ \)は，
\[
\begin{eqnarray}
m&=&\frac {V}{V_{\mathrm {m}}} \\[ 5pt ] &=&\frac {R+r}{r} \\[ 5pt ] &=&1+\frac {R}{r} \\[ 5pt ] \end{eqnarray}
\] となります。よって，倍率器の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
m&=&1+\frac {R}{r} \\[ 5pt ] \frac {R}{r}&=&m-1 \\[ 5pt ] R&=&\left( m-1\right) r\\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(a)解答：(1)
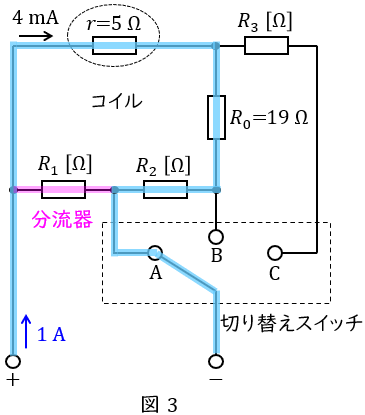
条件Ⅰにおいて，切り替えスイッチを\( \ \mathrm {A} \ \)にしたとき，電流は図3の示すように流れ，分流器が\( \ R_{1} \ \mathrm {[\Omega ]} \ \)であることがわかる。
コイルに流れる電流を求める分流の法則より，
\[
\begin{eqnarray}
4 &=&\frac {R_{1}}{R_{1}+r+R_{0}+R_{2}}\times 1 \ 000 \\[ 5pt ] 1&=&\frac {R_{1}}{R_{1}+5+19+R_{2}}\times 250 \\[ 5pt ] R_{1}+R_{2}+24 &=&250R_{1} \\[ 5pt ] 249R_{1}-R_{2} &=&24　・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。

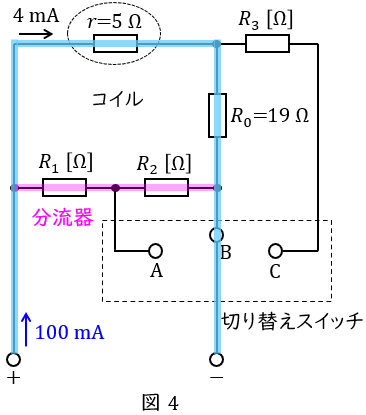
次に，条件Ⅱにおいて，切り替えスイッチを\( \ \mathrm {B} \ \)にしたとき，電流は図4の示すように流れ，分流器が\( \ R_{1} \ \mathrm {[\Omega ]} \ \)及び\( \ R_{2} \ \mathrm {[\Omega ]} \ \)であることがわかる。
コイルに流れる電流を求める分流の法則より，
\[
\begin{eqnarray}
4 &=&\frac {R_{1}+R_{2}}{R_{1}+R_{2}+r+R_{0}}\times 100 \\[ 5pt ] 1&=&\frac {R_{1}+R_{2}}{R_{1}+R_{2}+5+19}\times 25 \\[ 5pt ] R_{1}+R_{2}+24 &=&25R_{1}+25R_{2} \\[ 5pt ] 24R_{1}+24R_{2} &=&24 \\[ 5pt ] R_{1}+R_{2} &=&1　・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。

よって，\( \ ①+② \ \)より，
\[
\begin{eqnarray}
250R_{1} &=&25 \\[ 5pt ] R_{1} &=&0.1 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，これを\( \ ② \ \)に代入すれば，
\[
\begin{eqnarray}
0.1+R_{2} &=&1 \\[ 5pt ] R_{2} &=&0.9 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
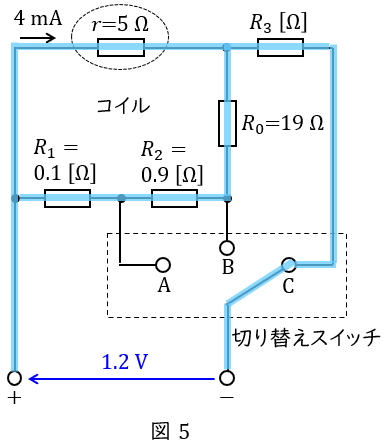
条件Ⅲにおいて，切り替えスイッチを\( \ \mathrm {C} \ \)にしたとき，電流は図5の示すように流れる。
コイルの最大電圧\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&4\times 10^{-3}\times 5 \\[ 5pt ] &=&0.02 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ r \ \mathrm {[\Omega ]} \ \)，\( \ R_{0} \ \mathrm {[\Omega ]} \ \)，\( \ R_{1} \ \mathrm {[\Omega ]} \ \)，\( \ R_{2} \ \mathrm {[\Omega ]} \ \)の合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)が，
\[
\begin{eqnarray}
R &=&\frac {r\left( R_{0}+R_{1}+R_{2}\right) }{r+R_{0}+R_{1}+R_{2}} \\[ 5pt ] &=&\frac {5\times \left( 19+0.1+0.9\right) }{5+19+0.1+0.9} \\[ 5pt ] &=&4 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であることから，\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)を求める分圧の法則より，
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&\frac {R}{R+R_{3}}\times 1.2 \\[ 5pt ] 0.02 &=&\frac {4}{4+R_{3}}\times 1.2 \\[ 5pt ] 1 &=&\frac {4}{4+R_{3}}\times 60 \\[ 5pt ] 4+R_{3} &=&240 \\[ 5pt ] R_{3} &=&236 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。