Contents
【問題】
【難易度】★☆☆☆☆(易しい)
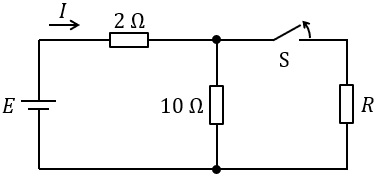
図のような直流回路において,スイッチ\( \ \mathrm {S} \ \)を閉じているとき,\( \ 2 \ \mathrm {\Omega } \ \)の抵抗を流れる電流は,スイッチ\( \ \mathrm {S} \ \)を開いたときの電流の\( \ 3 \ \)倍であった。\( \ R \ \)の値\( \ \mathrm {[\Omega ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 2.5 \ \) (2) \( \ 3.5 \ \) (3) \( \ 0.5 \ \) (4) \( \ 1.5 \ \) (5) \( \ 4.5 \ \)
【ワンポイント解説】
スイッチ開閉前後の電流値の変化から,未知の抵抗の抵抗値を求める問題です。
電気回路の基本問題から一歩進んだレベルですが,電験としては比較的解きやすい問題となります。基本公式に忠実に丁寧に解くようにしましょう。
本問は平成8年問5からの再出題となります。
1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時,それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。
①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
スイッチ\( \ \mathrm {S} \ \)を閉じているときの合成抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{1}&=&2+\frac {10R}{10+R} \\[ 5pt ]
&=&\frac {2\left( 10+R\right) +10R}{10+R} \\[ 5pt ]
&=&\frac {20+12R}{10+R} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 2 \ \mathrm {\Omega } \ \)の抵抗を流れる電流\( \ I_{1} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{1}&=&\frac {E}{R_{1}} \\[ 5pt ]
&=&\frac {10+R}{20+12R}E \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,スイッチ\( \ \mathrm {S} \ \)を開いているときの合成抵抗\( \ R_{2} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{2}&=&2+10 \\[ 5pt ]
&=&12 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 2 \ \mathrm {\Omega } \ \)の抵抗を流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{2}&=&\frac {E}{R_{2}} \\[ 5pt ]
&=&\frac {E}{12} \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より\( \ I_{1}=3I_{2} \ \)であるから,
\[
\begin{eqnarray}
\frac {10+R}{20+12R}E&=&3\cdot \frac {E}{12} \\[ 5pt ]
\frac {10+R}{20+12R}&=&\frac {1}{4} \\[ 5pt ]
4\left( 10+R\right) &=&20+12R \\[ 5pt ]
40+4R &=&20+12R \\[ 5pt ]
8R &=&20 \\[ 5pt ]
R &=&2.5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは