《理論》〈電磁気〉[H23:問3]磁界中に置かれた導体に働く電磁力に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，磁界中に置かれた導体に働く電磁力に関する記述である。

電流が流れている長さ$\ L \ \mathrm {[m]} \ $の直線導体を磁束密度が一様な磁界中に置くと，フレミングの$\ \fbox {　 （ア） 　} \ $の法則に従い，導体には電流の向きにも磁界の向きにも直角な電磁力が働く。直線導体の方向を変化させて，電流の方向が磁界の方向と同じになれば，導体に働く力の大きさは$\ \fbox {　 （イ） 　} \ $となり，直角になれば，$\ \fbox {　 （ウ） 　} \ $となる。力の大きさは，電流の$\ \fbox {　 （エ） 　} \ $に比例する。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

$$\begin{array}{ccccc} & （ア） & （イ） & （ウ） & （エ） \\ \hline (1) & 　左　手　 & 　最　大　 & 　零　　　 & 　2　乗　 \\ \hline (2) & 　左　手　 & 　零　　　 & 　最　大　 & 　2　乗　 \\ \hline (3) & 　右　手　 & 　零　　　 & 　最　大　 & 　1　乗　 \\ \hline (4) & 　右　手　 & 　最　大　 & 　零　　　 & 　2　乗　 \\ \hline (5) & 　左　手　 & 　零　　　 & 　最　大　 & 　1　乗　 \\ \hline \end{array}$$

【ワンポイント解説】

導体に働く電磁力に関する問題です。
フレミングの左手の法則，右手の法則とも電験では必須の内容となるので，よく勉強しておくようにしましょう。

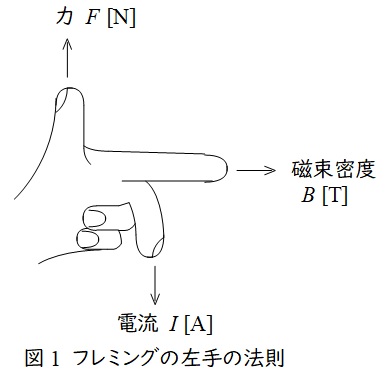
1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ$\ B \ \mathrm {[T]} \ $，電流の大きさ$\ I \ \mathrm {[A]} \ $，直線状導体の長さを$\ l \ \mathrm {[m]} \ $とすると，導体に発生する電磁力$\ F \ \mathrm {[N]} \ $は，

$$\begin{eqnarray} F &=&BIl \\[ 5pt ] \end{eqnarray}$$ となります。

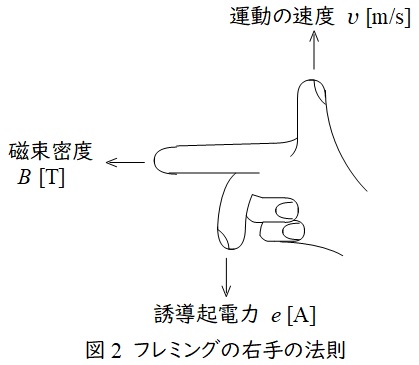
2.フレミングの右手の法則
親指を導体の運動方向，人差し指を磁界（磁束密度）の方向にすると，中指の方向に誘導起電力が発生するという法則で，磁束密度の大きさを$\ B \ \mathrm {[T]} \ $，導体の速度を$\ v \ \mathrm {[m／s]} \ $，導体の長さを$\ l \ \mathrm {[m]} \ $とすると，誘導起電力の大きさ$\ e \ \mathrm {[V]} \ $は，

$$\begin{eqnarray} e &=& Blv \\[ 5pt ] \end{eqnarray}$$ となります。

【解答】

解答：(5)
(ア)
ワンポイント解説「1.フレミングの左手の法則」の通り，磁界中に置かれた導体に働く電磁力に関するものは，フレミングの左手の法則となります。

(イ)
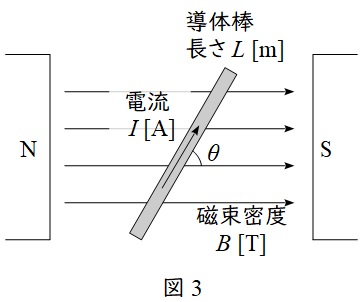
問題に沿って図を描くと図3のようになり，フレミングの左手の法則により，導体に働く電磁力$\ F \ $は，

$$\begin{eqnarray} F &=&BIl\sin \theta \\[ 5pt ] \end{eqnarray}$$ となります。したがって，電流の方向が磁界の方向と同じすなわち図3において$\ \theta =0 \ $のときは$\ \sin \theta =0 \ $となり，電磁力$\ F \ $は零となります。

(ウ)
（イ）と同様，図3において電流の方向が磁界の方向と直角すなわち$\ \theta =\displaystyle \frac {\pi }{2} \ $になれば，$\ \sin \theta =1 \ $となり，電磁力$\ F \ $は最大となります。

(エ)
ワンポイント解説「1.フレミングの左手の法則」の通り，力の大きさは電流の大きさの1乗に比例します。