《理論》〈電磁気〉[H29:問2]平行平板コンデンサの静電エネルギーに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

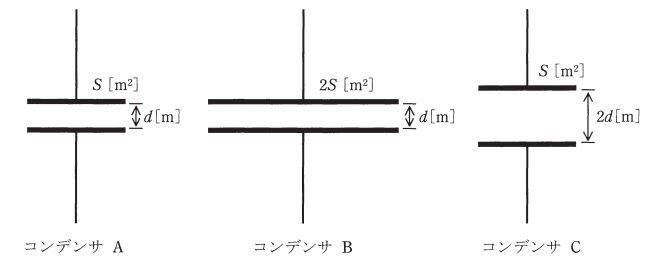
極板の面積\( \ S \left[ \mathrm {m^{2}}\right] \ \)，極板間の距離\( \ d \left[ \mathrm {m}\right] \ \)の平行板コンデンサ\( \ \mathrm {A} \ \)，極板の面積\( \ 2S \left[ \mathrm {m^{2}}\right] \ \)，極板間の距離\( \ d \left[ \mathrm {m}\right] \ \)の平行板コンデンサ\( \ \mathrm {B} \ \)及び極板の面積\( \ S \left[ \mathrm {m^{2}}\right] \ \)，極板間の距離\( \ 2d \left[ \mathrm {m}\right] \ \)の平行板コンデンサ\( \ \mathrm {C} \ \)がある。各コンデンサは，極板間の電界の強さが同じ値となるようにそれぞれ直流電源で充電されている。各コンデンサをそれぞれの直流電源から切り離した後，全コンデンサを同じ極性で並列に接続し，十分時間が経ったとき，各コンデンサに蓄えられる静電エネルギーの総和の値\( \ \left[ \mathrm {J}\right] \ \)は、並列に接続する前の総和の値\( \ \left[ \mathrm {J}\right] \ \)の何倍になるか。その倍率として，最も近いものを次に(1)～(5)のうちから一つ選べ。

ただし，各コンデンサの極板間の誘電率は同一であり，端効果は無視できるものとする。

　(1)　0.77　　(2)　0.91　　(3)　1.00　　(4)　1.09　　(5)　1.31

【ワンポイント解説】

平行平板コンデンサに係る公式をきちんと把握しており，かつ正確に計算しなければならないため，やや難しめの問題となっています。問題慣れすると，容量の異なるコンデンサを並列接続すると静電エネルギーは失われると判断できるようになるため，その時点で(1)か(2)の二択に絞ることができます。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.平行平板コンデンサの静電容量\( \ C \ \)
平板間の誘電率を\( \ \varepsilon \ \)，平板の面積を\( \ S \ \)，平板間の間隔を\( \ d \ \)とすると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon S}{d} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

3.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
平板間の間隔を\( \ d \ \)とすると，
\[
\begin{eqnarray}
E &=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

4.コンデンサの合成静電容量\( \ C_{0} \ \)
静電容量\( \ C_{1} \ \)と\( \ C_{2} \ \)の合成静電容量\( \ C_{0} \ \)は以下の通りとなります。
①並列時
\[
\begin{eqnarray}
C_{0} &=&C_{1}+C_{2} \\[ 5pt ] \end{eqnarray}
\] ②直列時
\[
\begin{eqnarray}
\frac {1}{C_{0}} &=&\frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ] \end{eqnarray}
\] すなわち，
\[
\begin{eqnarray}
C_{0} &=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] \end{eqnarray}
\]

5.平行平板コンデンサの静電エネルギー\( \ W \ \)
平行平板コンデンサの静電エネルギー\( \ W \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
各コンデンサ間の極板の誘電率を\( \ \varepsilon \ \)として，各コンデンサ\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)，\( \ \mathrm {C} \ \)の静電容量\( \ C_{\mathrm {A}} \ \)，\( \ C_{\mathrm {B}} \ \)，\( \ C_{\mathrm {C}} \ \)を求めると，
\[
\begin{eqnarray}
C_{\mathrm {A}}&=&\frac {\varepsilon S}{d} \\[ 5pt ] C_{\mathrm {B}}&=&\frac {2\varepsilon S}{d} \\[ 5pt ] C_{\mathrm {C}}&=&\frac {\varepsilon S}{2d} \\[ 5pt ] \end{eqnarray}
\] となる。題意より各コンデンサの極板間の電界の強さは同じ値であるから，その値を\( \ E \ \)として，各コンデンサ\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)，\( \ \mathrm {C} \ \)の電圧\(V_{\mathrm {A}}\)，\(V_{\mathrm {B}}\)，\(V_{\mathrm {C}}\)を求めると，
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&V_{\mathrm {B}}=Ed \\[ 5pt ] V_{\mathrm {C}}&=&2Ed \\[ 5pt ] \end{eqnarray}
\] となる。よって，各コンデンサ\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)，\( \ \mathrm {C} \ \)に蓄えられる電荷\(Q_{\mathrm {A}}\)，\(Q_{\mathrm {B}}\)，\(Q_{\mathrm {C}}\)は，
\[
\begin{eqnarray}
Q_{\mathrm {A}}&=&C_{\mathrm {A}}V_{\mathrm {A}} \\[ 5pt ] &=&\frac {\varepsilon S}{d}\cdot Ed \\[ 5pt ] &=&\varepsilon SE \\[ 5pt ] Q_{\mathrm {B}}&=&C_{\mathrm {B}}V_{\mathrm {B}} \\[ 5pt ] &=&\frac {2\varepsilon S}{d}\cdot Ed \\[ 5pt ] &=&2\varepsilon SE \\[ 5pt ] Q_{\mathrm {C}}&=&C_{\mathrm {C}}V_{\mathrm {C}} \\[ 5pt ] &=&\frac {\varepsilon S}{2d}\cdot 2Ed \\[ 5pt ] &=&\varepsilon SE \\[ 5pt ] \end{eqnarray}
\] となり，各コンデンサ\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)，\( \ \mathrm {C} \ \)に蓄えられる静電エネルギー\( \ W_{\mathrm {A}} \ \)，\( \ W_{\mathrm {B}} \ \)，\( \ W_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {A}}&=&\frac {1}{2}Q_{A}V_{A} \\[ 5pt ] &=&\frac {1}{2}\varepsilon SE\cdot Ed \\[ 5pt ] &=&\frac {1}{2}\varepsilon SE^{2}d \\[ 5pt ] W_{\mathrm {B}}&=&\frac {1}{2}Q_{\mathrm {B}}V_{\mathrm {B}} \\[ 5pt ] &=&\frac {1}{2}2\varepsilon SE\cdot Ed \\[ 5pt ] &=&\varepsilon SE^{2}d \\[ 5pt ] W_{\mathrm {C}}&=&\frac {1}{2}Q_{\mathrm {C}}V_{\mathrm {C}} \\[ 5pt ] &=&\frac {1}{2}\varepsilon SE\cdot 2Ed \\[ 5pt ] &=&\varepsilon SE^{2}d \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，並列接続前の各コンデンサに蓄えられる静電エネルギーの総和\( \ W_{0} \ \)は，
\[
\begin{eqnarray}
W_{0}&=&W_{\mathrm {A}}+W_{\mathrm {B}}+W_{\mathrm {C}} \\[ 5pt ] &=&\frac {1}{2}\varepsilon SE^{2}d +\varepsilon SE^{2}d +\varepsilon SE^{2}d \\[ 5pt ] &=&\frac {5}{2}\varepsilon SE^{2}d \\[ 5pt ] \end{eqnarray}
\] となる。
次に，各コンデンサを並列接続し，十分時間が経過した後の合計静電容量\( \ C \ \)は，
\[
\begin{eqnarray}
C&=&C_{\mathrm {A}}+C_{\mathrm {B}}+C_{\mathrm {C}} \\[ 5pt ] &=&\frac {\varepsilon S}{d}+\frac {2\varepsilon S}{d}+\frac {\varepsilon S}{2d} \\[ 5pt ] &=&\frac {7\varepsilon S}{2d} \\[ 5pt ] \end{eqnarray}
\] となる。一方，接続前後にて蓄えられる電荷量は変化がないので，その合計電荷量を\( \ Q \ \)とすると，
\[
\begin{eqnarray}
Q&=&Q_{\mathrm {A}}+Q_{\mathrm {B}}+Q_{\mathrm {C}} \\[ 5pt ] &=&\varepsilon SE+2\varepsilon SE+\varepsilon SE \\[ 5pt ] &=&4\varepsilon SE \\[ 5pt ] \end{eqnarray}
\] となる。よって，接続後に蓄えられる静電エネルギー\( \ W_{1} \ \)は，
\[
\begin{eqnarray}
W_{1}&=&\frac {Q^{2}}{2C} \\[ 5pt ] &=&\frac {\left( 4\varepsilon SE\right) ^{2}}{\displaystyle 2\frac {7\varepsilon S}{2d}} \\[ 5pt ] &=&\frac {16}{7}\varepsilon SE^{2}d \\[ 5pt ] \end{eqnarray}
\] と求められる。以上から，蓄えられる静電エネルギーの比は，
\[
\begin{eqnarray}
\frac {W_{1}}{W_{0}}&=&\frac {\displaystyle \frac {16}{7}\varepsilon SE^{2}d}{\displaystyle \frac {5}{2}\varepsilon SE^{2}d} \\[ 5pt ] &=&\frac {32}{35} \\[ 5pt ] &≒&0.914　→　0.91 \\[ 5pt ] \end{eqnarray}
\] となる。