《機械》〈回転機〉[H27:問5]同期発電機の同期インピーダンスに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

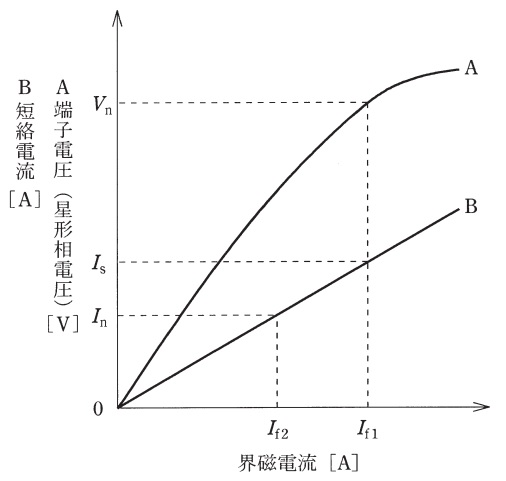
図は，同期発電機の無負荷飽和曲線(\(\mathrm {A}\))と短絡曲線(\(\mathrm {B}\))を示している。図中で\(V_{\mathrm {n}}\mathrm {[V]}\)は端子電圧(星形相電圧)の定格値，\(I_{\mathrm {n}}\mathrm {[A]}\)は定格電流，\(I_{\mathrm {s}}\mathrm {[A]}\)は無負荷で定格電圧を発生するときの界磁電流と等しい界磁電流における短絡電流である。この発電機の百分率同期インピーダンス\(z_{\mathrm {s}}\mathrm {[％]}\)を示す式として，正しいものを次の(1)～(5)のうちから一つ選べ。

(1)　\(\displaystyle \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}\times 100\)　　(2)　\(\displaystyle \frac {V_{\mathrm {n}}}{I_{\mathrm {n}}}\times 100\)　　(3)　\(\displaystyle \frac {I_{\mathrm {n}}}{I_{\mathrm {f2}}}\times 100\)

(4)　\(\displaystyle \frac {V_{\mathrm {n}}}{I_{\mathrm {f1}}}\times 100\)　　(5)　\(\displaystyle \frac {I_{\mathrm {f2}}}{I_{\mathrm {f1}}}\times 100\)

【ワンポイント解説】

無負荷飽和曲線と三相短絡曲線は非常によく出題される内容です。三相短絡曲線は曲線ですが，ほぼ直線に近いので，電験の問題では直線として扱います。短絡比及び同期インピーダンスとの関係をよく理解しておいて下さい。

1.短絡比\(K_{\mathrm {s}}\)
問題図の各値を使用し，短絡比\(K_{\mathrm {s}}\)を表すと，
\[
K_{\mathrm {s}}=\frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}}
\] となります。

2.同期インピーダンス\(Z_{\mathrm {s}}\)
問題図の各値を使用し，同期インピーダンス\(Z_{\mathrm {s}}\)を表すと，
\[
Z_{\mathrm {s}}=\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt{3}}}{I_{\mathrm {s}}}=\frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {s}}}
\] となります。

3．百分率同期インピーダンス\(z_{\mathrm {s}}\)
百分率同期インピーダンス\(z_{\mathrm {s}}\)は，同期インピーダンス\(Z_{\mathrm {s}}\)を用いて表すと，
\[
\begin{eqnarray}
z_{\mathrm {s}}&=&\frac {Z_{\mathrm {s}}}{Z_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {s}}}}{\frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {n}}}}\times 100 \\[ 5pt ] &=&\frac {I_{\mathrm {n}}}{I_{\mathrm {s}}}\times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
ワンポイント解説「3．百分率同期インピーダンス\(z_{\mathrm {s}}\)」の通り，
\[
z_{\mathrm {s}}=\frac {I_{\mathrm {n}}}{I_{\mathrm {s}}}\times 100
\] であり，問題図より，\(\displaystyle \frac {I_{\mathrm {n}}}{I_{\mathrm {s}}}=\frac {I_{\mathrm {f2}}}{I_{\mathrm {f1}}}\)であるから，
\[
z_{\mathrm {s}}=\frac {I_{\mathrm {f2}}}{I_{\mathrm {f1}}}\times 100
\] と求められる。