《理論》〈電磁気〉[H26:問3]環状鉄心に絶縁電線を巻いて作った磁気回路に関する論説問題

【問題】

【難易度】★★☆☆☆（やや易しい）

環状鉄心に絶縁電線を巻いて作った磁気回路に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。

(1)　磁気抵抗は，磁束の通りにくさを表している。毎ヘンリー\(\mathrm {\left[ H^{-1}\right] }\)は，磁気抵抗の単位である。

(2)　電気抵抗が導体断面積に反比例するように，磁気抵抗は，鉄心断面積に反比例する。

(3)　鉄心の透磁率が大きいほど，磁気抵抗は小さくなる。

(4)　起磁力が同じ場合，鉄心の磁気抵抗が大きいほど，鉄心を通る磁束は小さくなる。

(5)　磁気回路における起磁力と磁気抵抗は，電気回路におけるオームの法則の電流と電気抵抗にそれぞれ対応する。

【ワンポイント解説】

例年受験生を苦しめる誤答選択問題の中では比較的易しめの問題となっています。磁気回路は，慣れてしまえば電気回路と同じように考えて解くことができます。

1.磁気回路のオームの法則
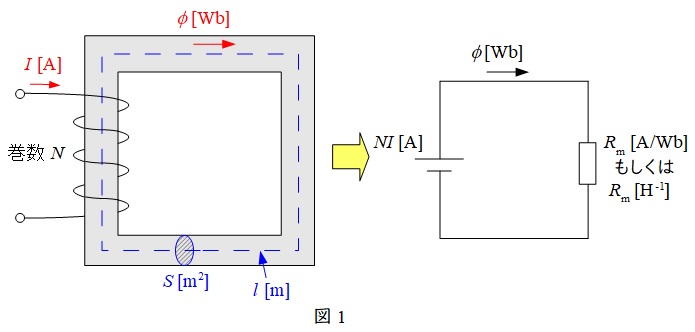
磁気回路は図1のように鉄心にコイルを巻きつけた環状ソレノイドについて，鉄心内の磁束\(\phi \)と起磁力\(NI\)，磁気抵抗\(R_{\mathrm {m}}\)との間に，
\[
\phi =\frac {NI}{R_{\mathrm {m}}}
\] の関係が成立し，電気回路のオームの法則と同等に扱うことができるというものです。
ここで，磁気抵抗\(R_{\mathrm {m}}\)は，鉄心内の透磁率\(\mu \)，断面積\(S\)，磁路の長さ\(l\)を用いて，
\[
R_{\mathrm {m}} =\frac {l}{\mu S}
\] で表すことができます。

【解答】

解答：(5)
(1)：正しい
問題文の通り，磁気抵抗は磁束の通りにくさを表しており，単位は，
\[
R_{\mathrm {m}} =\frac {l}{\mu S}　→　\frac {\mathrm {\left[ m\right] }}{\mathrm {\left[ H/m \right] \left[ m^{2}\right]}} =\mathrm {\left[ H^{-1}\right] }
\] となります。

(2)：正しい
ワンポイント解説「1.磁気回路のオームの法則」の通り，磁気抵抗\(R_{\mathrm {m}}\)は，鉄心の断面積\(S\)に反比例します。

(3)：正しい
ワンポイント解説「1.磁気回路のオームの法則」の通り，鉄心の透磁率\(\mu \)が大きいほど，磁気抵抗\(R_{\mathrm {m}}\)は小さくなります。

(4)：正しい
ワンポイント解説「1.磁気回路のオームの法則」の通り，鉄心の磁気抵抗\(R_{\mathrm {m}}\)が大きいほど，鉄心を通る磁束\(\phi \)は小さくなります。

(5)：誤り
ワンポイント解説「1.磁気回路のオームの法則」の通り，磁気回路における起磁力と磁気抵抗は，電気回路におけるオームの法則の起電力と電気抵抗にそれぞれ対応します。