Contents
【問題】
【難易度】★★★★☆(やや難しい)
実効値\( \ V \ \mathrm {[V]} \ \),角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)の交流電圧源,\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗\( \ \mathrm {R} \ \),インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル\( \ \mathrm {L} \ \),静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサ\( \ \mathrm {C} \ \)からなる共振回路に関する記述として,正しいものと誤りのものの組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\( \ \mathrm {\left( a\right) } \ \) \( \ \mathrm {RLC} \ \)直列回路の共振状態において,\( \ \mathrm {L} \ \)と\( \ \mathrm {C} \ \)の端子間電圧の大きさはともに\( \ \mathrm {0} \ \)である。
\( \ \mathrm {\left( b\right) } \ \) \( \ \mathrm {RLC} \ \)並列回路の共振状態において,\( \ \mathrm {L} \ \)と\( \ \mathrm {C} \ \)に電流は流れない。
\( \ \mathrm {\left( c\right) } \ \) \( \ \mathrm {RLC} \ \)直列回路の共振状態において交流電圧源を流れる電流は,\( \ \mathrm {RLC} \ \)並列回路の共振状態において交流電圧源を流れる電流と等しい。
\[
\begin{array}{cccc}
& \mathrm {\left( a\right) } & \mathrm {\left( b\right) } & \mathrm {\left( c\right) } \\
\hline
(1) & 誤り & 誤り & 正しい \\
\hline
(2) & 誤り & 正しい & 誤り \\
\hline
(3) & 正しい & 誤り & 誤り \\
\hline
(4) & 誤り & 誤り & 誤り \\
\hline
(5) & 正しい & 正しい & 正しい \\
\hline
\end{array}
\]
【ワンポイント解説】
直列共振及び並列共振の特徴に関する問題です。
共振周波数のメカニズムを理解せず公式だけ暗記していると解けない問題です。
直列共振と並列共振の違いや特徴を理解しておくようにしましょう。
1.直列回路の共振回路
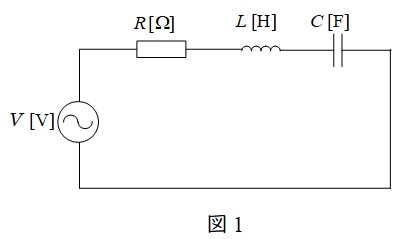
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \)は,角周波数を\( \ \omega \ \)とすると,
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,インピーダンスが最も小さくなるためには,上式の虚数部が零である必要があります。よって,共振角周波数\( \ \omega _{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ]
\omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ]
\omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ]
\omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,共振周波数を\( \ f_{\mathrm {c}} \ \)とすると,\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より,
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.並列回路の共振回路
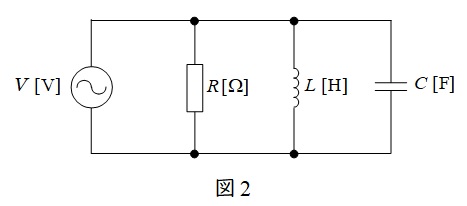
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \)は,角周波数を\( \ \omega \ \)とすると,
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ]
&=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\]
となり,アドミタンスが最も小さくなるためには,上式の虚数部が零である必要があります。よって,共振角周波数\( \ \omega _{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ]
\omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ]
\omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ]
\omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,共振周波数を\( \ f_{\mathrm {c}} \ \)とすると,\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より,
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
(a)誤り
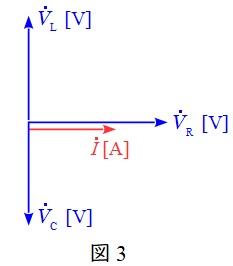
図1の\( \ \mathrm {RLC} \ \)直列回路のベクトル図を描くと図3のようになり,直列共振状態においてはインダクタンスの電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)とコンデンサの電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)の大きさが等しいため合計すると\( \ \mathrm {0} \ \)となります。
それぞれの端子間電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)及び\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)が\( \ \mathrm {0} \ \)になるわけではありません。
(b)誤り
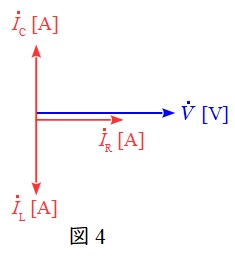
図2の\( \ \mathrm {RLC} \ \)並列回路のベクトル図を描くと図4のようになり,並列共振状態においてはインダクタンスを流れる電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \)とコンデンサを流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)の大きさが等しいため合計すると\( \ \mathrm {0} \ \)となります。
それぞれの素子に流れる電流が\( \ \mathrm {0} \ \)になるわけではありません。
(c)正しい
ワンポイント解説「1.直列回路の共振回路」の通り,\( \ \mathrm {RLC} \ \)直列回路の共振状態においては,合成インピーダンスが\( \ R \ \mathrm {[\Omega ]} \ \)となるため,電源を流れる電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=& \frac {V}{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,ワンポイント解説「2.並列回路の共振回路」の通り,\( \ \mathrm {RLC} \ \)並列回路の共振状態においては,合成アドミタンスが\( \ \displaystyle \frac {1}{R} \ \mathrm {[\Omega ]} \ \)となるため,電源を流れる電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=& \frac {1}{R}\times V \\[ 5pt ]
&=& \frac {V}{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,直列共振及び並列共振においても電源を流れる電流の大きさは等しくなります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは