《理論》〈電気回路〉[R3:問8]正弦波交流回路の瞬時値に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

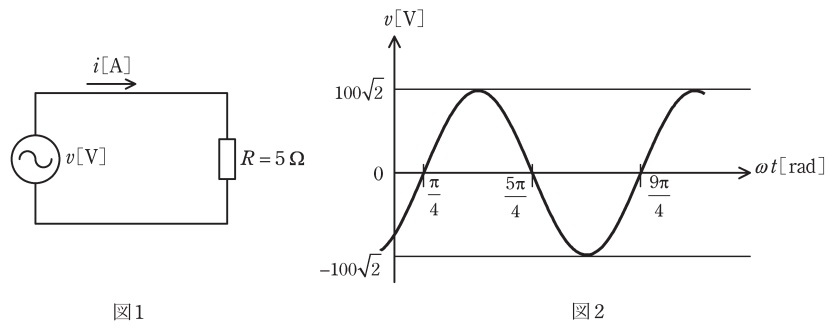
図1の回路において，図2のような波形の正弦波交流電圧\( \ v \ \mathrm {[V]} \ \)を抵抗\( \ 5 \ \mathrm {\Omega } \ \)に加えたとき，回路を流れる電流の瞬時値\( \ i \ \mathrm {[A]} \ \)を表す式として，正しいものを次の(1)～(5)のうちから一つ選べ。ただし，電源の周波数を\( \ 50 \ \mathrm {Hz} \ \)，角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)，時間を\( \ t \ \mathrm {[s]} \ \)とする。

　(1)　\( \ 20\sqrt {2}\sin \left( 50\pi t-\displaystyle \frac {\pi }{4}\right) \ \)

　(2)　\( \ 20\sin \left( 50\pi t+\displaystyle \frac {\pi }{4}\right) \ \)

　(3)　\( \ 20\sin \left( 100\pi t-\displaystyle \frac {\pi }{4}\right) \ \)

　(4)　\( \ 20\sqrt {2}\sin \left( 100\pi t+\displaystyle \frac {\pi }{4}\right) \ \)

　(5)　\( \ 20\sqrt {2}\sin \left( 100\pi t-\displaystyle \frac {\pi }{4}\right) \ \)

【ワンポイント解説】

正弦波交流の瞬時値に関する問題です。
重要な内容ではありますが，どちらかというと数学的な要素が強いので，電験では出題されにくい傾向がありました。
交流の概念を理解するのにはとても良い問題であると思うので，理解しておくようにしましょう。

1.正弦波交流の基本
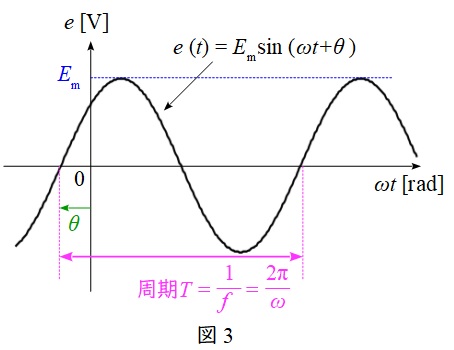
正弦波交流は図3に示されるような波形の交流です。
振幅の大きさ（最大値）を\( \ E_{\mathrm {m}} \ \mathrm {[V]} \ \)，角速度を\( \ \omega \ \mathrm {[rad / s]} \ \)，時間を\( \ t \ \mathrm {[s]} \ \)，初期位相を\( \ \theta \ \mathrm {[rad]} \ \)とすれば，瞬時値\( \ e\left( t \right) \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( \omega t +\theta \right) \\[ 5pt ] \end{eqnarray}
\] となり，波形の周期\( \ T \ \mathrm {[s]} \ \)は，周波数を\( \ f \ \mathrm {[Hz]} \ \)とすると，
\[
\begin{eqnarray}
T &=&\frac {1}{f}=\frac {2\pi }{\omega } \\[ 5pt ] \end{eqnarray}
\] の関係があるので，\( \ \omega =2\pi f \ \)となり，
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( 2\pi f t +\theta \right) \\[ 5pt ] \end{eqnarray}
\] と表現することもできます。

【解答】

解答：(5)
ワンポイント解説「1.正弦波交流の基本」の通り，図2より，\( \ v\left( t \right) \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
v\left( t \right) &=&V_{\mathrm {m}}\sin \left( \omega t +\theta \right) \\[ 5pt ] \end{eqnarray}
\] で表され，
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&100\sqrt {2} \ \mathrm {[V]} \\[ 5pt ] \omega &=&2\pi f \\[ 5pt ] &=&2\pi \times 50 \\[ 5pt ] &=&100\pi \ \mathrm {[rad / s]} \\[ 5pt ] \theta &=&-\frac {\pi }{4} \ \mathrm {[rad]} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
v\left( t \right) &=&100\sqrt {2}\sin \left( 100\pi t -\frac {\pi }{4} \right) \\[ 5pt ] \end{eqnarray}
\] となる。したがって，線路を流れる電流\( \ i\left( t \right) \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
i\left( t \right) &=&\frac {v\left( t \right) }{R} \\[ 5pt ] &=&\frac {\displaystyle 100\sqrt {2}\sin \left( 100\pi t -\frac {\pi }{4} \right) }{5} \\[ 5pt ] &=&20\sqrt {2}\sin \left( 100\pi t -\frac {\pi }{4} \right) \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。