《理論》〈電子理論〉[R3:問12]平等電界及び平等磁界中の電子の運動に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

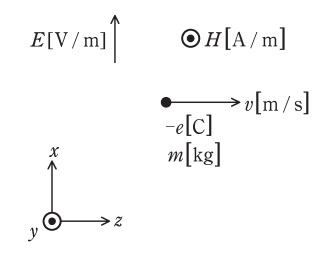
図のように，\( \ x \ \)方向の平等電界\( \ E \ \mathrm {[V / m]} \ \)，\( \ y \ \)方向の平等磁界\( \ H \ \mathrm {[A / m]} \ \)が存在する真空の空間において，電荷\( \ -e \ \mathrm {[C]} \ \)，質量\( \ m \ \mathrm {[kg]} \ \)をもつ電子が\( \ z \ \)方向の初速度\( \ v \ \mathrm {[m / s]} \ \)で放出された。この電子が等速直線運動をするとき，\( \ v \ \)を表す式として，正しいものを次の(1)～(5)のうちから一つ選べ。ただし，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)，真空の透磁率を\( \ \mu _{0} \ \mathrm {[H / m]} \ \)とし，重力の影響を無視する。

また，電子の質量は変化しないものとする。図中の\( \ \odot \ \)は紙面に垂直かつ手前の向きを表す。

　(1)　\( \ \displaystyle \frac {\varepsilon _{0}E}{\mu _{0}H} \ \)　　(2)　\( \ \displaystyle \frac {E}{H} \ \)　　(3)　\( \ \displaystyle \frac {E}{\mu _{0}H} \ \)　　(4)　\( \ \displaystyle \frac {H}{\varepsilon _{0}E} \ \)　　(5)　\( \ \displaystyle \frac {\mu _{0}H}{E} \ \)

【ワンポイント解説】

電界により電子に働く力と磁界により電子に働く力を組み合わせた問題です。
電子の運動はそれぞれ個別に出題されることが多かったですが，本問はその両方の知識を必要とします。
最も出題されやすいのは平成24年問12に出題されているサイクロトロン運動なので，合わせて見ておくようにして下さい。

1.電荷に働く力の大きさ
一様な電界\( \ E \ \)が電荷\( \ q \ \)にかかっているとき，この電荷\( \ q \ \)に働く力の大きさ\( \ F \ \)は，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] となります。

2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \)，電子の速度\( \ v \ \)，電子の電荷を\( \ e \ \)とすると，電子にかかるローレンツ力\( \ F \ \)は
\[
\begin{eqnarray}
F &=&evB \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合，動く向きが電流の向きと逆になるので，中指の向きに注意するようにしましょう。

【解答】

解答：(3)
電界\( \ E \ \mathrm {[V / m]} \ \)により，電子に加わる力\( \ F_{\mathrm {E}} \ \mathrm {[N]} \ \)は，ワンポイント解説「1.電荷に働く力の大きさ」の通り，
\[
\begin{eqnarray}
F_{\mathrm {E}} &=&eE　（下向き） \\[ 5pt ] \end{eqnarray}
\] であり，磁界\( \ H \ \mathrm {[A / m]} \ \)により，電子に加わる力\( \ F_{\mathrm {H}} \ \mathrm {[N]} \ \)は，ワンポイント解説「2.フレミングの左手の法則」の通り，
\[
\begin{eqnarray}
F_{\mathrm {H}} &=&evB \\[ 5pt ] &=&\mu _{0}evH　（上向き） \\[ 5pt ] \end{eqnarray}
\] である。電子が等速直線運動をするためには，\( \ F_{\mathrm {E}} \ \)と\( \ F_{\mathrm {H}} \ \)がつりあっていなければならないので，
\[
\begin{eqnarray}
F_{\mathrm {E}} &=&F_{\mathrm {H}} \\[ 5pt ] eE&=&\mu _{0}evH \\[ 5pt ] E&=&\mu _{0}vH \\[ 5pt ] v&=&\frac {E}{\mu _{0}H} \\[ 5pt ] \end{eqnarray}
\] と求められる。