《理論》〈電気回路〉[R01:問6]直流回路の抵抗で消費される電力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図に示す直流回路は，\( \ 100 \ \mathrm {V} \ \)の直流電圧源に直流電流計を介して\( \ 10 \ \mathrm {\Omega } \ \)の抵抗が接続され，\( \ 50 \ \mathrm {\Omega } \ \)の抵抗と抵抗\( \ R \ \mathrm {[\Omega ]} \ \)が接続されている。電流計は\( \ 5 \ \mathrm {A} \ \)を示している。抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費される電力の値\( \ \mathrm {[W]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。なお，電流計の内部抵抗は無視できるものとする。

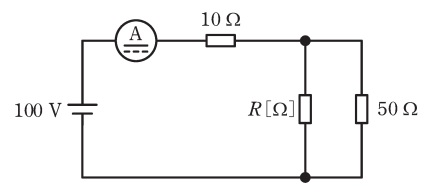
　(1)　\( \ 2 \ \)　　(2)　\( \ 10 \ \)　　(3)　\( \ 20 \ \)　　(4)　\( \ 100 \ \)　　(5)　\( \ 200 \ \)　　

【ワンポイント解説】

キルヒホッフの法則を使いこなせればそれほど難しい問題ではありません。基本的な公式を理解し順序立てて解くようにしましょう。

1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが，法則を説明できる必要はなく，計算で使いこなせることが重要です。
①第1法則（電流則）
　回路の接続点に流入する電流の和と流出する電流の和が等しい。

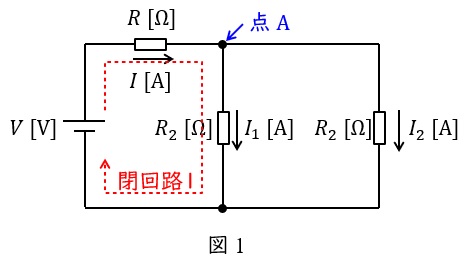
　図1で言えば，例えば接続点\( \ \mathrm {A} \ \)において，
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ] \end{eqnarray}
\] 　となります。

②第2法則（電圧則）
　任意の閉回路において，起電力の総和と抵抗の電圧降下の和は等しい。

　図1で言えば，例えば閉回路\( \ 1 \ \)において，
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ] \end{eqnarray}
\] 　となります。

2.抵抗での消費電力
ある抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に電圧\( \ V \ \mathrm {[V]} \ \)をかけたとき抵抗に電流\( \ I \ \mathrm {[A]} \ \)が流れたとすると，\( \ R \ \mathrm {[\Omega ]} \ \)での消費電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&VI \\[ 5pt ] \end{eqnarray}
\] となります。オームの法則\( \ V=RI \ \)より上式は，
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ] &=&\frac {V^{2}}{R} \\[ 5pt ] \end{eqnarray}
\] と変形できます。

【関連する「電気の神髄」記事】

　　キルヒホッフの法則とその解釈

【解答】

解答：(5)
\( \ 10 \ \mathrm {\Omega } \ \)の抵抗に流れる電流\( \ I_{10}=5 \ \mathrm {[A]} \ \)であるから，\( \ 10 \ \mathrm {\Omega } \ \)の抵抗にかかる電圧\( \ V_{10} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{10}&=&10\times I_{10} \\[ 5pt ] &=&10\times 5 \\[ 5pt ] &=&50 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R \ \mathrm {[\Omega ]} \ \)及び\( \ 50 \ \mathrm {\Omega } \ \)にかかる電圧は\( \ 100-50=50 \ \mathrm {[V]} \ \)となる。
これより，\( \ 50 \ \mathrm {\Omega } \ \)の抵抗に流れる電流\( \ I_{50} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{50}&=&\frac {50}{50} \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)は，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
I_{\mathrm {R}}&=&5-1 \\[ 5pt ] &=&4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
R&=&\frac {50}{I_{\mathrm {R}}} \\[ 5pt ] &=&\frac {50}{4} \\[ 5pt ] &=&12.5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.抵抗での消費電力」より，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費される電力\( \ P_{\mathrm {R}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {R}}&=&RI_{\mathrm {R}}^{2} \\[ 5pt ] &=&12.5\times 4^{2} \\[ 5pt ] &=&200 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。