《理論》〈電磁気〉[H22:問2]平行平板コンデンサに誘電体を挿入したときの特性に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

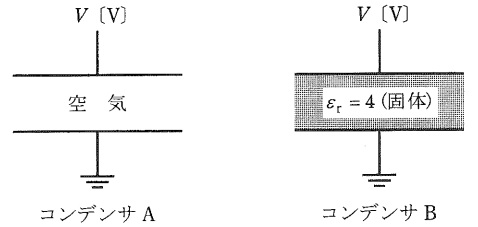
図に示すように，電極板面積と電極板間隔がそれぞれ同一の\( \ 2 \ \)種類の平行平板コンデンサがあり，一方を空気コンデンサ\( \ \mathrm {A} \ \)，他方を固体誘電体（比誘電率\( \ \varepsilon _{\mathrm {r}}=4 \ \)）が満たされたコンデンサ\( \ \mathrm {B} \ \)とする。両コンデンサにおいて，それぞれ一方の電極に直流電圧\( \ V \ \mathrm {[V]} \ \)を加え，他方の電極を接地したとき，コンデンサ\( \ \mathrm {B} \ \)の内部電界\( \ \mathrm {[V / m]} \ \)及び電極板上に蓄えられた電荷\( \ \mathrm {[C]} \ \)はコンデンサ\( \ \mathrm {A} \ \)のそれぞれ何倍となるか。その倍率として，正しいものを組み合わせたのは次のうちどれか。

ただし，空気の比誘電率を\( \ 1 \ \)とし，コンデンサの端効果は無視できるものとする。

\[
\begin{array}{ccc}
& 　内部電界　 & 　電　荷　 \\
\hline
(1) & 　1　 & 　4　 \\
\hline
(2) & 　4　 & 　4　 \\
\hline
(3) & 　\displaystyle \frac {1}{4}　 & 　4　 \\
\hline
(4) & 　4　 & 　1　 \\
\hline
(5) & 　1　 & 　1　 \\
\hline
\end{array}
\]

【ワンポイント解説】

平行平板コンデンサの内部電界と蓄えられる電荷の導出に関する問題です。
本問で扱う公式はいずれも平行平板コンデンサにおける重要公式となりますので，使いこなせるようにしておいて下さい。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)，極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \)，極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

3.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると，極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
①内部電界
各コンデンサの極板間距離を\( \ d \ \mathrm {[m]} \ \)とする。
コンデンサ\( \ \mathrm {A} \ \)の内部電界\( \ E_{\mathrm {A}} \ \mathrm {[V / m]} \ \)及びコンデンサ\( \ \mathrm {B} \ \)の内部電界\( \ E_{\mathrm {B}} \ \mathrm {[V / m]} \ \)は，ワンポイント解説「3.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
E_{\mathrm {A}}&=&\frac {V}{d} \\[ 5pt ] E_{\mathrm {B}}&=&\frac {V}{d} \\[ 5pt ] &=&E_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ E_{\mathrm {B}} \ \)は\( \ E_{\mathrm {A}} \ \)の\( \ 1 \ \)倍と求められる。

②電荷
コンデンサ\( \ \mathrm {A} \ \)の静電容量\( \ C_{\mathrm {A}} \ \mathrm {[F]} \ \)及びコンデンサ\( \ \mathrm {B} \ \)の静電容量\( \ C_{\mathrm {B}} \ \mathrm {[F]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)，極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \)，極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると，ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り，
\[
\begin{eqnarray}
C_{\mathrm {A}} &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] C_{\mathrm {B}} &=&\frac {4\varepsilon _{0}S}{d} \\[ 5pt ] &=&4C_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となる。よって，それぞれのコンデンサに蓄えられる電荷\( \ Q_{\mathrm {A}} \ \mathrm {[C]} \ \)及び\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)は，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
Q_{\mathrm {A}} &=&C_{\mathrm {A}}V \\[ 5pt ] Q_{\mathrm {B}} &=&C_{\mathrm {B}}V \\[ 5pt ] &=&4C_{\mathrm {A}}V \\[ 5pt ] &=&4Q_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ Q_{\mathrm {B}} \ \)は\( \ Q_{\mathrm {A}} \ \)の\( \ 4 \ \)倍と求められる。