《理論》〈電気回路〉[H22:問6]抵抗を繋ぎ変えた場合の直流回路の電流値に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

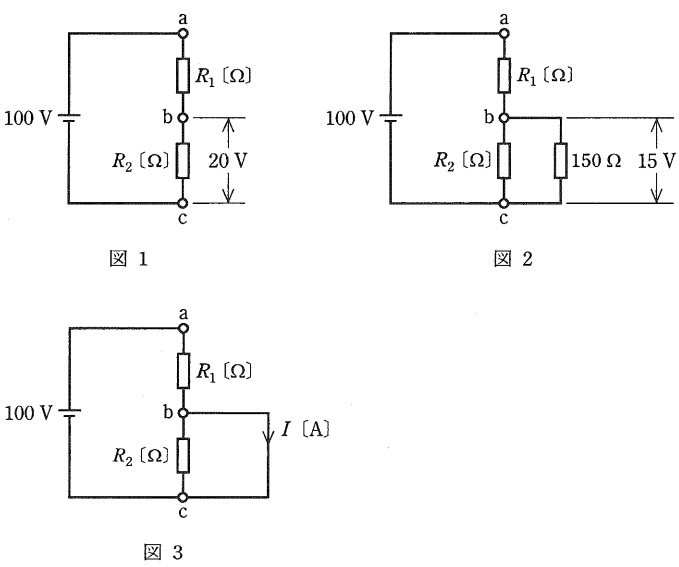
図1の直流回路において，端子\( \ \mathrm {a-c} \ \)間に直流電圧\( \ 100 \ \mathrm {[V]} \ \)を加えたところ，端子\( \ \mathrm {b-c} \ \)間の電圧は\( \ 20 \ \mathrm {[V]} \ \)であった。また，図2のように端子\( \ \mathrm {b-c} \ \)間に\( \ 150 \ \mathrm {[\Omega ]} \ \)の抵抗を並列に追加したとき，端子\( \ \mathrm {b-c} \ \)間の端子電圧は\( \ 15 \ \mathrm {[V]} \ \)であった。いま，図3のように端子\( \ \mathrm {b-c} \ \)間を短絡したとき，電流\( \ I \ \mathrm {[A]} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ 0 \ \)　　(2)　\( \ 0.10 \ \)　　(3)　\( \ 0.32 \ \)　　(4)　\( \ 0.40 \ \)　　(5)　\( \ 0.67 \ \)

【ワンポイント解説】

図1及び図2の条件から各抵抗値を導き出して，図3の回路を解く問題です。
一つ一つ丁寧に解いていけばそれほど難しくありませんので，基本公式に忠実に解くようにしましょう。
解答はオーソドックスかつできるだけ早く解ける方法を掲載していますが，正答が導き出せればどのような解き方でも問題ありません。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則
①分圧の法則
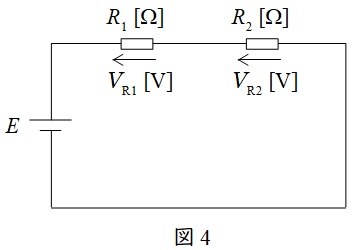
図4に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

②分流の法則
図5に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(4)
図1において，分圧の法則を適用すると，
\[
\begin{eqnarray}
20&=&\frac {R_{2}}{R_{1}+R_{2}}\times 100 \\[ 5pt ] 1&=&\frac {R_{2}}{R_{1}+R_{2}}\times 5 \\[ 5pt ] R_{1}+R_{2}&=&5R_{2} \\[ 5pt ] R_{1}&=&4R_{2} \\[ 5pt ] \end{eqnarray}
\] となり，図2において，\( \ R_{1} \ \)に流れる電流と\( \ R_{2} \ \)及び\( \ 150 \ \mathrm {[\Omega ]} \ \)の抵抗に流れる電流の合計値は等しいことから，
\[
\begin{eqnarray}
\frac {100-15}{R_{1}}&=&\frac {15}{R_{2}}+\frac {15}{150} \\[ 5pt ] \frac {85}{R_{1}}&=&\frac {15}{\displaystyle \frac {R_{1}}{4}}+\frac {1}{10} \\[ 5pt ] \frac {85}{R_{1}}&=&\frac {60}{R_{1}}+\frac {1}{10} \\[ 5pt ] \frac {25}{R_{1}}&=&\frac {1}{10} \\[ 5pt ] R_{1}&=&250 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，図3における電流\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I&=&\frac {100}{R_{1}} \\[ 5pt ] &=&\frac {100}{250} \\[ 5pt ] &=&0.40 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。