《理論》〈電気回路〉[H26:問8]交流回路の並列接続に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図の交流回路において，電源を流れる電流\(I \ \mathrm {[A]}\)の大きさが最小となるように静電容量\(C \ \mathrm {[F]}\)の値を調整した。このときの回路の力率の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

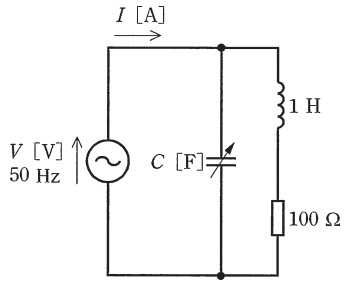
(1)　\(0.11\)　　(2)　\(0.50\)　　(3)　\(0.71\)　　(4)　\(0.87\)　　(5)　\(1\)

【ワンポイント解説】

電気の勉強に習熟してくると1秒で解けてしまう問題です。本問の場合，電流は力率が1の時最小となることを知っていれば，下記のような計算は不要と思います。

1.リアクトル\(L\)とコンデンサ\(C\)のインピーダンス
インダクタンス\(L\)のリアクトルと静電容量\(C\)のコンデンサのインピーダンスとアドミタンスは，電源の周波数を\(f\)とすると，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L ，&{\dot Y}_{\mathrm {L}}=&\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} ，&{\dot Y}_{\mathrm {C}}=&\mathrm {j}\omega C \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
リアクトルと抵抗の合成インピーダンス\(\dot Z\)は，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L \\[ 5pt ] \end{eqnarray}
\] であるから，コンデンサを含めた合成アドミタンス\(\dot Y\)は，
\[
\begin{eqnarray}
\dot Y&=&\mathrm {j}\omega C+\frac {1}{\dot Z} \\[ 5pt ] &=&\mathrm {j}\omega C+\frac {1}{R+\mathrm {j}\omega L} \\[ 5pt ] &=&\mathrm {j}\omega C+\frac {R-\mathrm {j}\omega L}{R^{2}+\left( \omega L\right) ^{2}} \\[ 5pt ] &=&\frac {R}{R^{2}+\left( \omega L\right) ^{2}} +\mathrm {j}\omega \left[ C-\frac {L}{R^{2}+\left( \omega L\right) ^{2}}\right] \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\(I=\left| \dot Y\right| V\)の関係があるので，\(I\)が最小となるためには，\(\left| \dot Y\right| \)が最小となる必要があり，\(C\)は虚数部のみの変数であるため，虚数部が\(0\)となれば最小となる。
よって，電流と電圧は同位相となり，力率は\(1\)となる。