《理論》〈電磁気〉[H22:問17]正三角形上に置かれた点電荷に働く力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

真空中において，図に示すように，一辺の長さが\( \ 6 \ \mathrm {[m]} \ \)の正三角形の頂点\( \ \mathrm {A} \ \)に\( \ 4\times 10^{-9} \ \mathrm {[C]} \ \)の正の点電荷が置かれ，頂点\( \ \mathrm {B} \ \)に\( \ -4\times 10^{-9} \ \mathrm {[C]} \ \)の負の点電荷が置かれている。正三角形の残る頂点を点\( \ \mathrm {C} \ \)とし，点\( \ \mathrm {C} \ \)より下した垂線と正三角形の辺\( \ \mathrm {AB} \ \)との交点を点\( \ \mathrm {D} \ \)として，次の(a)及び(b)に答えよ。

ただし，クーロンの法則の比例定数を\( \ 9\times 10^{9} \ \mathrm {[N\cdot m^{2} / C^{2}]} \ \)とする。

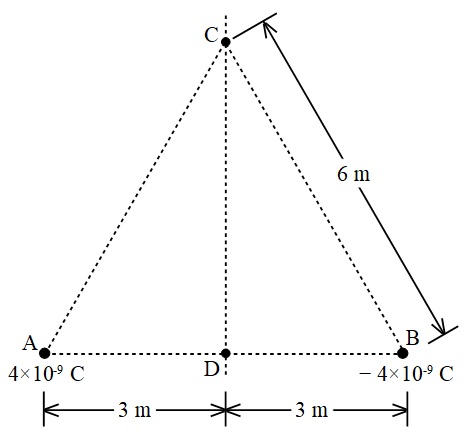
(a)　まず，\( \ q_{0} \ \mathrm {[C]} \ \)の正の点電荷を点\( \ \mathrm {C} \ \)に置いたときに，この正の点電荷に働く力の大きさは\( \ F_{\mathrm {C}} \ \mathrm {[N]} \ \)であった。次に，この正の点電荷を点\( \ \mathrm {D} \ \)に移動したときに，この正の点電荷に働く力の大きさは\( \ F_{\mathrm {D}} \ \mathrm {[N]} \ \)であった。力の大きさの比\( \ \displaystyle \frac {F_{\mathrm {C}}}{F_{\mathrm {D}}} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ \displaystyle \frac {1}{8} \ \)　　(2)　\( \ \displaystyle \frac {1}{4} \ \)　　(3)　\( \ 2 \ \)　　(4)　\( \ 4 \ \)　　(5)　\( \ 8 \ \)

(b)次に，\( \ q_{0} \ \mathrm {[C]} \ \)の正の点電荷を点\( \ \mathrm {D} \ \)から点\( \ \mathrm {C} \ \)の位置に戻し，強さが\( \ 0.5 \ \mathrm {[V / m]} \ \)の一様な電界を辺\( \ \mathrm {AB} \ \)に平行に点\( \ \mathrm {B} \ \)から点\( \ \mathrm {A} \ \)の向きに加えた。このとき，\( \ q_{0} \ \mathrm {[C]} \ \)の正の点電荷に電界の向きと逆の向きに\( \ 2\times 10^{-9} \ \mathrm {[N]} \ \)の大きさの力が働いた。正の点電荷\( \ q_{0} \ \mathrm {[C]} \ \)の値として，正しいのは次のうちどれか。

　　(1)　\( \ \displaystyle \frac {4}{3}\times 10^{-9} \ \)　　(2)　\( \ 2\times 10^{-9} \ \)　　(3)　\( \ 4\times 10^{-9} \ \)　　

　　(4)　\( \ \displaystyle \frac {4}{3}\times 10^{-8} \ \)　　(5)　\( \ 2\times 10^{-8} \ \)

【ワンポイント解説】

クーロンの法則を使用した点電荷に働く力に関する問題です。
電験で出題された場合，合格者のほとんどが完答してくる問題と言えます。クーロンの法則は本番までに必ずマスターするようにして下さい。
また，問題の読み間違え等には十分に注意しましょう。

1.クーロンの法則
真空中で距離\( \ r \ \mathrm {[m]} \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \mathrm {[C]} \ \)，\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)に加わる力\( \ F \ \mathrm {[N]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると，
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。このとき，\( \ Q_{\mathrm {A}} \ \)，\( \ Q_{\mathrm {B}} \ \)の\( \ + \ \)\( \ – \ \)の符号が同符号である場合には斥力（反発する力），異符号である場合には引力（引き合う力）が働きます。

2.真空中の電界の大きさ
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)をおいた時，電荷から距離\( \ r \ \mathrm {[m]} \ \)離れた場所の電界の大きさ\( \ E \ \mathrm {[N / C]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると，
\[
\begin{eqnarray}
E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。この場所に電荷\( \ q \ \mathrm {[C]} \ \)の電荷を置けば，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] の力が働きます。

【解答】

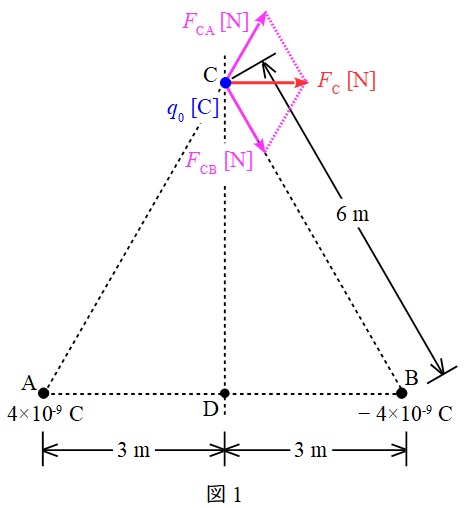
(a)解答：(1)
図1のように，\( \ q_{0} \ \mathrm {[C]} \ \)の正の点電荷を点\( \ \mathrm {C} \ \)に置いたとき，それぞれの電荷から働く力を\( \ F_{\mathrm {CA}} \ \mathrm {[N]} \ \)及び\( \ F_{\mathrm {CB}} \ \mathrm {[N]} \ \)とする。
\( \ F_{\mathrm {CA}} \ \mathrm {[N]} \ \)及び\( \ F_{\mathrm {CB}} \ \mathrm {[N]} \ \)の大きさは，ワンポイント解説「1.クーロンの法則」の通り，
\[
\begin{eqnarray}
F_{\mathrm {CA}} &=&\frac {q_{\mathrm {A}}q_{\mathrm {C}}}{4\pi \varepsilon _{0}r_{\mathrm {CA}}^{2}} \\[ 5pt ] &=&9\times 10^{9}\times \frac {4\times 10^{-9}\times q_{0}}{6^{2}} \\[ 5pt ] &=&q_{0} \ \mathrm {[N]} \\[ 5pt ] F_{\mathrm {CB}} &=&\frac {q_{\mathrm {B}}q_{\mathrm {C}}}{4\pi \varepsilon _{0}r_{\mathrm {CB}}^{2}} \\[ 5pt ] &=&9\times 10^{9}\times \frac {4\times 10^{-9}\times q_{0}}{6^{2}} \\[ 5pt ] &=&q_{0} \ \mathrm {[N]} \\[ 5pt ] \end{eqnarray}
\] となる。図1より，ベクトル合成を考えれば\( \ F_{\mathrm {C}}=F_{\mathrm {CA}}=F_{\mathrm {CB}} \ \)であるから，\( \ F_{\mathrm {C}}=q_{0} \ \mathrm {[N]} \ \)と求められる。

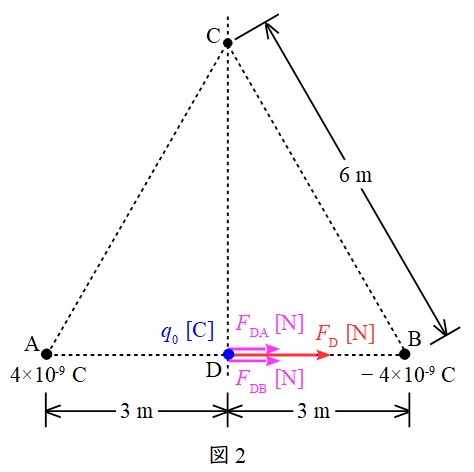
次に，図2のように，\( \ q_{0} \ \mathrm {[C]} \ \)の正の点電荷を点\( \ \mathrm {D} \ \)に置いたとき，それぞれの電荷から働く力を\( \ F_{\mathrm {DA}} \ \mathrm {[N]} \ \)及び\( \ F_{\mathrm {DB}} \ \mathrm {[N]} \ \)とする。
\( \ F_{\mathrm {DA}} \ \mathrm {[N]} \ \)及び\( \ F_{\mathrm {DB}} \ \mathrm {[N]} \ \)の大きさは，ワンポイント解説「1.クーロンの法則」の通り，
\[
\begin{eqnarray}
F_{\mathrm {DA}} &=&\frac {q_{\mathrm {A}}q_{\mathrm {D}}}{4\pi \varepsilon _{0}r_{\mathrm {DA}}^{2}} \\[ 5pt ] &=&9\times 10^{9}\times \frac {4\times 10^{-9}\times q_{0}}{3^{2}} \\[ 5pt ] &=&4q_{0} \ \mathrm {[N]} \\[ 5pt ] F_{\mathrm {DB}} &=&\frac {q_{\mathrm {B}}q_{\mathrm {D}}}{4\pi \varepsilon _{0}r_{\mathrm {DB}}^{2}} \\[ 5pt ] &=&9\times 10^{9}\times \frac {4\times 10^{-9}\times q_{0}}{3^{2}} \\[ 5pt ] &=&4q_{0} \ \mathrm {[N]} \\[ 5pt ] \end{eqnarray}
\] となる。図2より，ベクトル合成を考えれば\( \ F_{\mathrm {D}}=F_{\mathrm {DA}}+F_{\mathrm {DB}} \ \)であるから，\( \ F_{\mathrm {D}}=8q_{0} \ \mathrm {[N]} \ \)と求められる。

以上から，
\[
\begin{eqnarray}
\frac {F_{\mathrm {C}}}{F_{\mathrm {D}}} &=&\frac {q_{0}}{8q_{0}} \\[ 5pt ] &=&\frac {1}{8} \\[ 5pt ] \end{eqnarray}
\] と求められる。

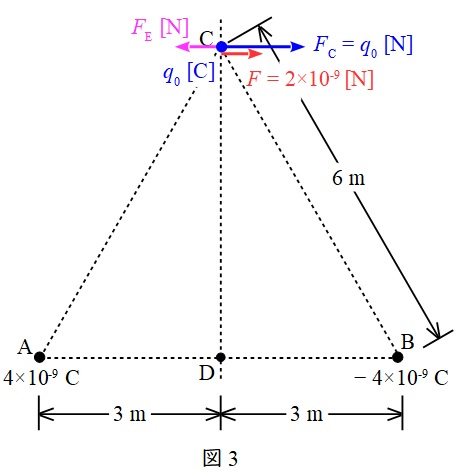
(b)解答：(3)
題意に沿って図を描くと図3の通りとなる。電界\( \ E=0.5 \ \mathrm {[V / m]} \ \)により，電荷に加わる力\( \ F_{\mathrm {E}} \ \mathrm {[N]} \ \)は，ワンポイント解説「2.真空中の電界の大きさ」の通り，
\[
\begin{eqnarray}
F_{\mathrm {E}} &=&q_{0}E \\[ 5pt ] &=&q_{0}\times 0.5 \\[ 5pt ] &=&0.5q_{0} \\[ 5pt ] \end{eqnarray}
\] となるので，ベクトル合成を考えれば，電荷に加わる力\( \ F=2\times 10^{-9} \ \mathrm {[N]} \ \)との関係から，
\[
\begin{eqnarray}
F &=&F_{\mathrm {C}}-F_{\mathrm {E}} \\[ 5pt ] 2\times 10^{-9} &=&q_{0}-0.5q_{0} \\[ 5pt ] 2\times 10^{-9}&=&0.5q_{0} \\[ 5pt ] q_{0}&=&4\times 10^{-9} \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] と求められる。