《理論》〈電子理論〉[R3:問18]トランジスタを用いた発振回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

発振回路について，次の(a)及び(b)の問に答えよ。
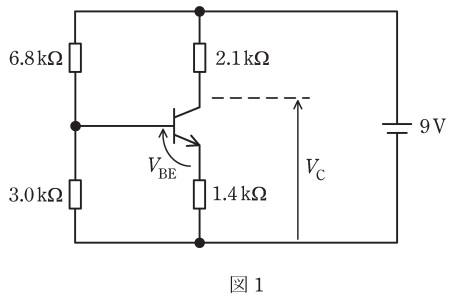
(a)　図1は，ある発振回路のコンデンサを開放し，同時にコイルを短絡した，直流分を求めるための回路図である。図中の電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。
　ただし，図中の\( \ V_{\mathrm {BE}} \ \)並びにエミッタ接地トランジスタの直流電流増幅率\( \ h_{\mathrm {FE}} \ \)をそれぞれ\( \ V_{\mathrm {BE}}=0.6 \ \mathrm {[V]} \ \)，\( \ h_{\mathrm {FE}}=100 \ \)とする。

　(1)　\( \ 3 \ \)　　(2)　\( \ 4 \ \)　　(3)　\( \ 5 \ \)　　(4)　　\( \ 6 \ \)　　(5)　\( \ 7 \ \)

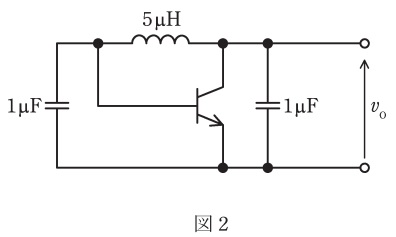
(b)　図2は，ある発振回路のトランジスタに接続されている，電極間のリアクタンスを示している。ただし，バイアス回路は省略している。この回路が発振するとき，発振周波数\( \ f_{0} \ \mathrm {[kHz]} \ \)はどの程度の大きさになるか，最も近いものを次の(1)～(5)のうちから一つ選べ。
　ただし，発振周波数は，図に示されている素子の値のみにより定まるとしてよい。

　(1)　\( \ 0.1 \ \)　　(2)　\( \ 1 \ \)　　(3)　\( \ 10 \ \)　　(4)　　\( \ 100 \ \)　　(5)　\( \ 1 \ 000 \ \)

【ワンポイント解説】

トランジスタを用いた発振回路に関する問題です。
発振回路は正弦波等の電気的振動を出力するための電子回路で，ラジオ等の搬送波として現在でも用いられています。
電験対策としては，発振条件を覚えておけば十分かと思います。

1.発振回路の発振条件
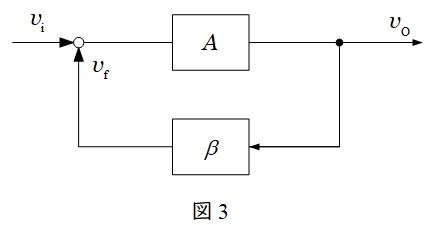
図1の回路において，演算増幅器\( \ A \ \)と帰還回路\( \ \beta \ \)とした時，
　　①\( \ A\beta ≧1 \ \)（振幅条件）
　　②\( \ A\beta \ \)の位相角が零（周波数条件）
を満たすとき，発振回路は発振を継続します。
本問においては接続されているコンデンサとリアクトルで上記②を満たせば発振すると考えれば良いです。

2.直列回路の共振回路
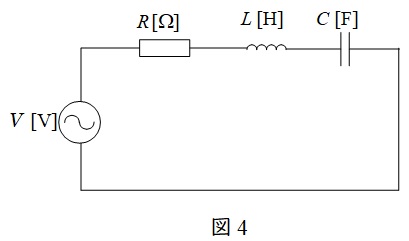
図4のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.並列回路の共振回路
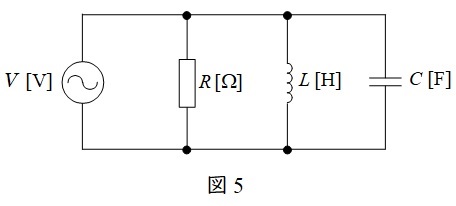
図5のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(4)
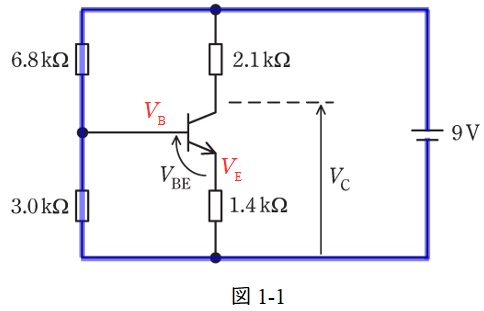
図1-1に示した閉回路に分圧の法則を適用すると，ベース電圧\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&\frac {3.0}{6.8+3.0}\times 9 \\[ 5pt ] &≒&2.755 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ V_{\mathrm {BE}}=0.6 \ \mathrm {[V]} \ \)であるから，エミッタ電圧\( \ V_{\mathrm {E}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {E}} &=&V_{\mathrm {B}}-V_{\mathrm {BE}} \\[ 5pt ] &=&2.755-0.6 \\[ 5pt ] &=&2.155 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，エミッタ電流\( \ I_{\mathrm {E}} \ \mathrm {[mA]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {E}} &=&\frac {V_{\mathrm {E}}}{1.4\times 10^{3}} \\[ 5pt ] &=&\frac {2.155}{1.4\times 10^{3}} \\[ 5pt ] &≒&1.539\times 10^{-3} \ \mathrm {[A]}　→　1.539 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ \displaystyle h_{\mathrm {FE}}=\frac {I_{\mathrm {C}}}{I_{\mathrm {B}}}=100 \ \)及び\( \ I_{\mathrm {E}}=I_{\mathrm {B}}+I_{\mathrm {C}} \ \)より，
\[
\begin{eqnarray}
I_{\mathrm {E}} &=&I_{\mathrm {B}}+I_{\mathrm {C}} \\[ 5pt ] &=&\frac {I_{\mathrm {C}}}{100}+I_{\mathrm {C}} \\[ 5pt ] &=&\frac {101}{100}I_{\mathrm {C}} \\[ 5pt ] I_{\mathrm {C}}&=&\frac {100}{101}I_{\mathrm {E}} \\[ 5pt ] &=&\frac {100}{101}\times 1.539 \\[ 5pt ] &≒&1.524 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] となるので，コレクタ電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {C}} &=&9-2.1\times 10^{3}I_{\mathrm {C}} \\[ 5pt ] &=&9-2.1\times 10^{3}\times 1.524\times 10^{-3} \\[ 5pt ] &≒&5.80 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
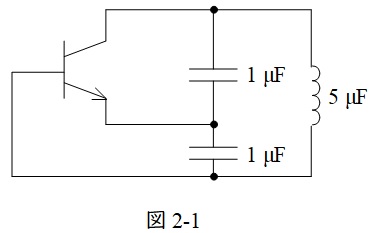
ワンポイント解説「1.発振回路の発振条件」より，回路が発振するためには，合成のリアクタンスが零とならなければならない。したがって，回路の共振周波数を求めればよい。図2-1のように回路を書き換えて，コンデンサの直列合成静電容量を求めると，
\[
\begin{eqnarray}
C &=&\frac {1\times 10^{-6}\times 1\times 10^{-6}}{1\times 10^{-6}+1\times 10^{-6}} \\[ 5pt ] &=&0.5\times 10^{-6} \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「3.並列回路の共振回路」の通り発振周波数を求めると，
\[
\begin{eqnarray}
f_{0} &=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] &=&\frac {1}{2\pi \sqrt {5\times 10^{-6}\times 0.5\times 10^{-6}}} \\[ 5pt ] &≒&101 \ 000 \ \mathrm {[Hz]}　→　101 \ \mathrm {[kHz]} \\[ 5pt ] \end{eqnarray}
\] と求められる。