《機械》〈パワーエレクトロニクス〉[H22:問16]単相全波整流回路の電圧・電流に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図には，バルブデバイスとしてサイリスタを用いた単相全波整流回路を示す。交流電源電圧を\( \ e=\sqrt {2}E \sin \omega t \ \mathrm {[V]} \ \)，単相全波整流回路出力の直流電圧を\( \ e_{\mathrm {d}} \ \mathrm {[V]} \ \)，サイリスタの電流を\( \ i_{\mathrm {T}} \ \mathrm {[A]} \ \)として，次の(a)及び(b)に答えよ。

ただし，重なり角などは無視し，平滑リアクトルにより直流電流は一定とする。

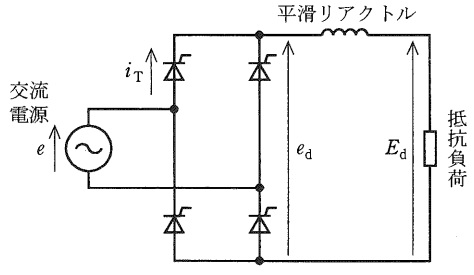
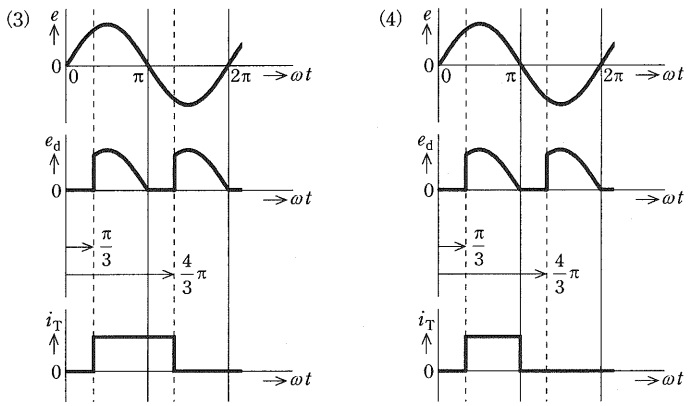
(a)　サイリスタの制御遅れ角\( \ \alpha \ \)が\( \ \displaystyle \frac {\pi }{3} \ \mathrm {[rad]} \ \)のときに，\( \ e \ \)に対する，\( \ e_{\mathrm {d}} \ \)，\( \ i_{\mathrm {T}} \ \)の波形として，正しいのは次のうちどれか。

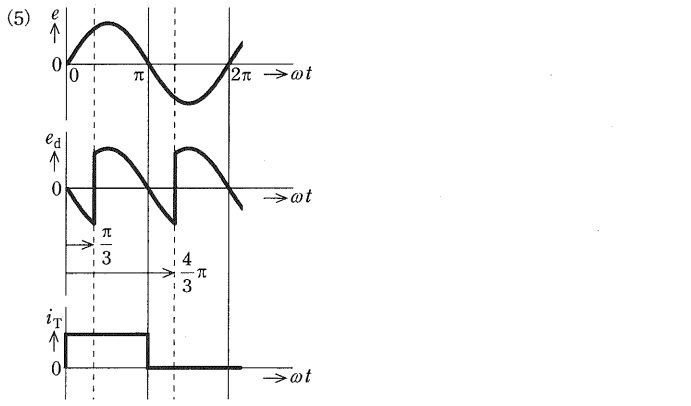
(b)　負荷抵抗にかかる出力の直流電圧\( \ E_{\mathrm {d}} \ \mathrm {[V]} \ \)は上記(a)に示された瞬時値波形の平均値となる。制御遅れ角\( \ \alpha \ \)を\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)としたときの電圧\( \ \mathrm {[V]} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ 0 \ \)　　(2)　\( \ \displaystyle \frac {\sqrt {2}}{\pi }E \ \)　　(3)　\( \ \displaystyle \frac {1}{2}E \ \)　　(4)　\( \ \displaystyle \frac {\sqrt {2}}{2}E \ \)　　(5)　\( \ \displaystyle \frac {2\sqrt {2}}{\pi }E \ \)

【ワンポイント解説】

サイリスタを用いた単相全波整流回路に関する問題です。
サイリスタがどのように動作し，平滑リアクトルがどのような作用をするかを理解すると，整流回路の問題は解きやすくなります。

1.単相サイリスタブリッジ整流回路の動作
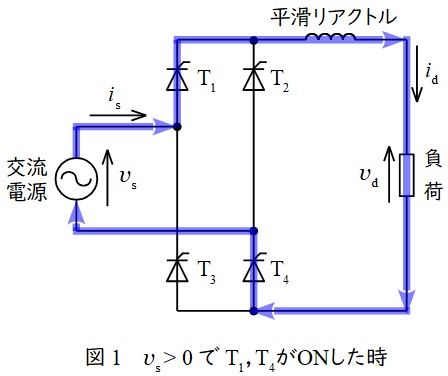
図1，図2に示す単相サイリスタブリッジ整流回路は以下のように動作します。

①\( \ v_{\mathrm {s}}＞0 \ \)でサイリスタ\( \ \mathrm {T}_{1} \ \)と\( \ \mathrm {T}_{4} \ \)がオンとなったとき
図1のように，電流は交流電源→\( \ \mathrm {T}_{1} \ \)→平滑リアクトル→負荷→\( \ \mathrm {T}_{4} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると，入力電圧\( \ v_{\mathrm {s}} \ \)と等しくなります。
\( \ v_{\mathrm {s}}＜0 \ \)になった以降も平滑リアクトルの容量がなくなるまで，負荷電流\( \ i_{\mathrm {d}} \ \)が流れることになります。

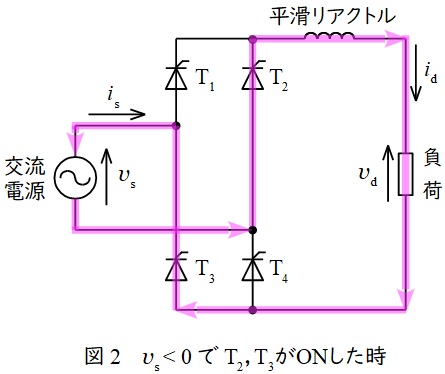
②\( \ v_{\mathrm {s}}＜0 \ \)でサイリスタ\( \ \mathrm {T}_{2} \ \)と\( \ \mathrm {T}_{3} \ \)がオンとなったとき
図2のように，電流は交流電源→\( \ \mathrm {T}_{2} \ \)→平滑リアクトル→負荷→\( \ \mathrm {T}_{3} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると，\( \ -v_{\mathrm {s}} \ \)となります。
\( \ v_{\mathrm {s}}＞0 \ \)になった以降も平滑リアクトルの容量がなくなるまで，負荷電流\( \ i_{\mathrm {d}} \ \)が流れることになります。

平滑リアクトルの容量が十分に大きいとすれば，\( \ i_{\mathrm {d}} \ \)はほぼ一定値となります。また，制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)で制御しているとすると平均出力電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は，交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {d}} &=& \frac {1}{\pi }\int _{\alpha }^{\pi +\alpha }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left[ -\cos \omega t\right] _{\alpha }^{\pi +\alpha } \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left\{ -\cos \left( \pi +\alpha \right) +\cos \alpha \right\} \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left( -\cos \pi \cos \alpha +\sin \pi \sin \alpha +\cos \alpha \right) \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left( \cos \alpha +0+\cos \alpha \right) \\[ 5pt ] &=& \frac {2\sqrt {2}}{\pi }V\cos \alpha \\[ 5pt ] &≃& 0.90V\cos \alpha \\[ 5pt ] \end{eqnarray}
\] となります。

※積分の考え方を使用しているので，\( \ 3 \ \)種としては結果を暗記することになります。

【解答】

(a)解答：(2)
ワンポイント解説「1.単相サイリスタブリッジ整流回路の動作」の通り，出力電圧はサイリスタが切り替わった\( \ \displaystyle \frac {\pi }{3} \ \mathrm {[rad]} \ \)及び\( \ \displaystyle \frac {4\pi }{3} \ \mathrm {[rad]} \ \)のタイミングで正負が入れ替わり，\( \ i_{\mathrm {T}} \ \)は\( \ \displaystyle \frac {\pi }{3} \ \mathrm {[rad]} \ \)から切り替わる\( \ \displaystyle \frac {4\pi }{3} \ \mathrm {[rad]} \ \)の間流れる。
したがって，波形として正しいのは(2)となる。

(b)解答：(1)
ワンポイント解説「1.単相サイリスタブリッジ整流回路の動作」の通り，\( \ \alpha = \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)のとき，出力電圧\( \ E_{\mathrm {d}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {d}} &≃& 0.90E\cos \alpha \\[ 5pt ] &=& 0.90V\cos \frac {\pi }{2} \\[ 5pt ] &=& 0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

※　(2)の解答の波形から\( \ \alpha = \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)の波形をイメージして平均値が零になると求めても大丈夫です。