《機械》〈電動機応用〉[R05上:問11]電動機と減速機を組み合わせた負荷の駆動に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

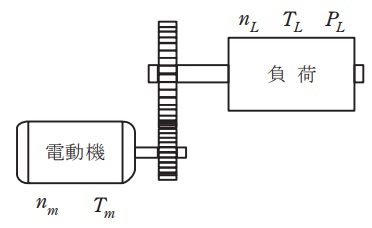
図に示すように，電動機が減速機と組み合わされて負荷を駆動している。このときの電動機の回転速度\( \ n_{m} \ \)が\( \ 1 \ 150 \ \mathrm {{min}^{-1}} \ \)，トルク\( \ T_{m} \ \)が \( \ 100 \ \mathrm {N\cdot m} \ \)であった。減速機の減速比が\( \ 8 \ \)，効率が\( \ 0.95 \ \)のとき，負荷の回転速度\( \ n_{L} \ \mathrm {[{min}^{-1}]} \ \)，軸トルク\( \ T_{L} \ \mathrm {[N\cdot m]} \ \)及び軸入力\( \ P_{L} \ \mathrm {[kW]} \ \)の値として，最も近いものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cccc}
& 　n_{L} \ \mathrm {[{min}^{-1}]}　 & 　T_{L} \ \mathrm {[N\cdot m]}　 & 　P_{L} \ \mathrm {[kW]}　 \\
\hline
(1) & 　136.6　 & 　11.9　 & 　11.4　 \\
\hline
(2) & 　143.8　 & 　760 \ \ 　　 & 　11.4　 \\
\hline
(3) & 　9 \ 200　　　 & 　760 \ \ 　　 & 　6 \ 992 \ \ 　　　 \\
\hline
(4) & 　143.8　 & 　11.9　 & 　11.4　 \\
\hline
(5) & 　9 \ 200　　　 & 　11.9　 & 　6 \ 992 \ \ 　　　 \\
\hline
\end{array}
\]

【ワンポイント解説】

電動機と減速機を組み合わせた負荷の駆動に関する問題です。
以下に公式を紹介しますが，公式を覚えるというよりも，図を見ながらメカニズムを理解し解けるようになるのが理想です。
本問は平成20年問11からの再出題となります。

1.減速機での回転速度，トルク
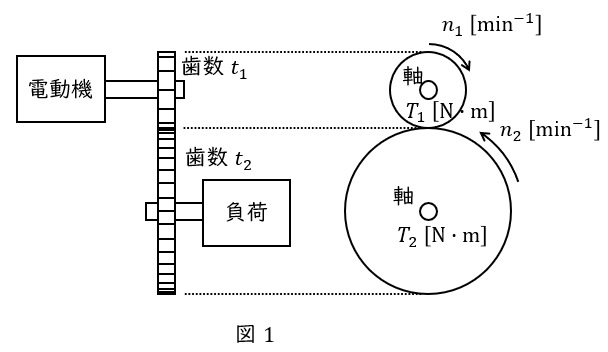
図1のように歯数\( \ t_{1} \ \)及び\( \ t_{2} \ \)の減速機があり，それぞれ電動機と負荷に繋いだときの電動機の回転速度\( \ n_{1} \ \mathrm {[{min}^{-1}]} \ \)，負荷の回転速度\( \ n_{2} \ \mathrm {[{min}^{-1}]} \ \)とすると，歯車の嚙み合う歯数は等しいことから，
\[
\begin{eqnarray}
n_{1}t_{1} &=&n_{2}t_{2} \\[ 5pt ] \frac {t_{2}}{t_{1}} &=& \frac {n_{1}}{n_{2}}=a \\[ 5pt ] \end{eqnarray}
\] となり，これを減速比といいます。減速機の効率を\( \ \eta \ \)，電動機の軸出力を\( \ P_{1} \ \mathrm {[W]} \ \)，負荷への軸入力を\( \ P_{2} \ \mathrm {[W]} \ \)とすると，
\[
\begin{eqnarray}
P_{2} &=&\eta P_{1} \\[ 5pt ] \end{eqnarray}
\] の関係があるため，電動機の軸トルク\( \ T_{1} \ \mathrm {[N\cdot m]} \ \)と負荷の軸トルク\( \ T_{2} \ \mathrm {[N\cdot m]} \ \)の関係は，それぞれの角速度を\( \ \omega _{1} \ \mathrm {[rad / s]} \ \)，\( \ \omega _{2} \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
\omega _{2}T_{2} &=&\eta \omega _{1}T_{1} \\[ 5pt ] \frac {2\pi n_{2}}{60}\cdot T_{2} &=&\eta \cdot \frac {2\pi n_{1}}{60}\cdot T_{1} \\[ 5pt ] n_{2} T_{2} &=&\eta n_{1}T_{1} \\[ 5pt ] T_{2} &=&\eta \cdot \frac {n_{1}}{n_{2}}\cdot T_{1} \\[ 5pt ] &=&\eta a T_{1} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
減速比\( \ a=8 \ \)であるから，負荷の回転速度\( \ n_{L} \ \mathrm {[{min}^{-1}]} \ \)は，ワンポイント解説「1.減速機での回転速度，トルク」の通り，
\[
\begin{eqnarray}
n_{L} &=&\frac {n_{m}}{a} \\[ 5pt ] &=&\frac {1 \ 150}{8} \\[ 5pt ] &=&143.75　→　143.8 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

電動機の軸出力\( \ P_{m} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{m} &=&\omega _{m}T_{m} \\[ 5pt ] &=&\frac {2\pi n_{m}}{60}\cdot T_{m} \\[ 5pt ] &=&\frac {2\pi \times 1 \ 150}{60}\times 100 \\[ 5pt ] &≒&12 \ 040 \ \mathrm {[W]}　→　12.04 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] であり，減速機の効率が\( \ \eta =0.95 \ \)であるから，負荷の軸入力\( \ P_{L} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{L} &=&\eta P_{m} \\[ 5pt ] &=&0.95\times 12.04 \\[ 5pt ] &≒&11.44　→　11.4 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

また，負荷の軸トルク\( \ T_{L} \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T_{L} &=&\frac {P_{m}}{\omega _{m}} \\[ 5pt ] &=&\frac {P_{m}}{\displaystyle \frac {2\pi n_{m}}{60}} \\[ 5pt ] &=&\frac {60P_{m}}{2\pi n_{m}} \\[ 5pt ] &=&\frac {60\times 11.44\times 10^{3}}{2\pi \times 143.75} \\[ 5pt ] &≒&760 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。