Contents
【問題】
【難易度】★★★☆☆(普通)
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),誘導性リアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)からなる平衡三相負荷(力率\( \ 80 \ \mathrm {%} \ \))に対称三相交流電源を接続した交流回路がある。次の(a)及び(b)の問に答えよ。
(a) 図1のように,\( \ \mathrm {Y} \ \)結線した平衡三相負荷に線間電圧\( \ 210 \ \mathrm {V} \ \)の三相電圧を加えたとき,回路を流れる線電流\( \ I \ \)は\( \ \displaystyle \frac {14}{\sqrt {3}} \ \mathrm {A} \ \)であった。負荷の誘導性リアクタンス\( \ X \ \)の値\( \ \mathrm {[\Omega ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
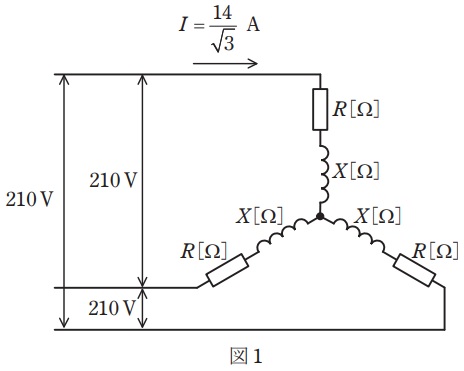
(1) \( \ 4 \ \) (2) \( \ 5 \ \) (3) \( \ 9 \ \) (4) \( \ 12 \ \) (5) \( \ 15 \ \)
(b) 図1の各相の負荷を使って\( \ \Delta \ \)結線し,図2のように相電圧\( \ 200 \ \mathrm {V} \ \)の対称三相電源に接続した。この平衡三相負荷の全消費電力の値\( \ \mathrm {[kW]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
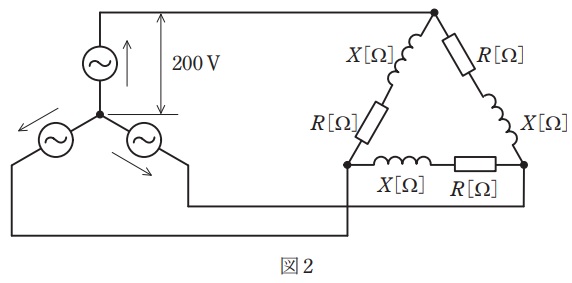
(1) \( \ 8 \ \) (2) \( \ 11.1 \ \) (3) \( \ 13.9 \ \) (4) \( \ 19.2 \ \) (5) \( \ 33.3 \ \)
【ワンポイント解説】
三相交流回路の\( \ \mathrm {Y} \ \)結線及び\( \ \Delta \ \)結線した回路における計算問題です。
三相平衡回路なので,一相分等価回路にしていくことを考えていきます。
本問は平成18年問15からの再出題となります。
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
となります。この関係をベクトル図に表すと,図3~図5となります。
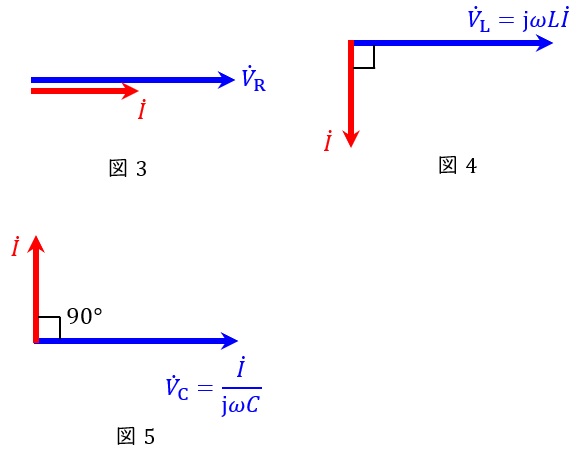
2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
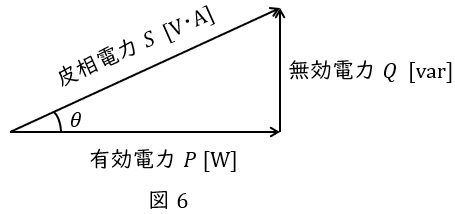
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \),リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び,図6のようにベクトル図を描きます。さらに,有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図6において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
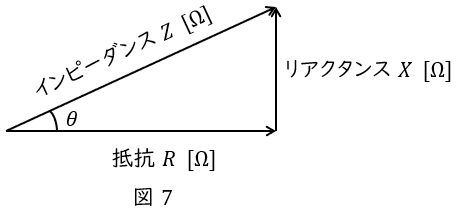
また,線路に電流\( \ I \ \mathrm {[A]} \ \)が流れているとき,皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \),有効電力\( \ P \ \mathrm {[W]} \ \),無効電力\( \ Q \ \mathrm {[var]} \ \)は,インピーダンスを\( \ Z \ \mathrm {[\Omega ]} \ \),抵抗を\( \ R \ \mathrm {[\Omega ]} \ \),リアクタンスを\( \ X \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ]
P &=&RI^{2} \\[ 5pt ]
Q &=&XI^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ Z \ \mathrm {[\Omega ]} \ \),\( \ R \ \mathrm {[\Omega ]} \ \),\( \ X \ \mathrm {[\Omega ]} \ \)に関しても電力と同様な図7のような関係を描くことができます。
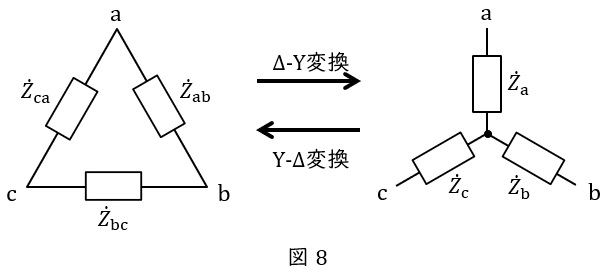
3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図8において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図8において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\]
となります。
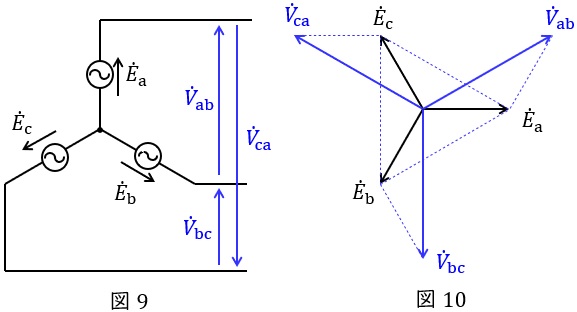
4.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図9のような三相対称電源がある時,線間電圧と相電圧の関係は図10のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)進みであることが分かります。
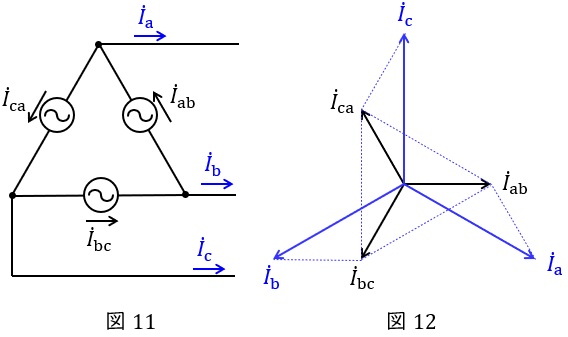
5.\( \ \Delta \ \)結線における相電流と線電流の関係
図11のような三相対称電源がある時,線電流と相電流の関係は図12のベクトル図のようになり,線電流の大きさは相電流の大きさと比較すると,
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ]
I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ]
I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)遅れであることが分かります。
【解答】
(a)解答:(3)
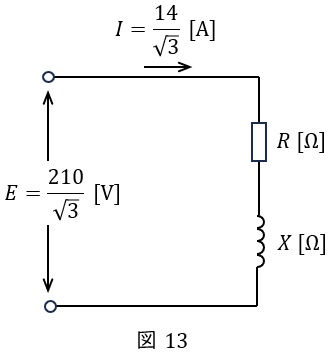
図1の各インピーダンスに加わる電圧は相電圧であり,その大きさはワンポイント解説「4.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り\( \ \displaystyle E=\frac {210}{\sqrt {3}} \ \mathrm {[V]} \ \)である。したがって,一相分等価回路は図13のようになる。
よって,負荷のインピーダンスの大きさ\( \ Z \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
Z &=&\frac {E}{I} \\[ 5pt ]
&=&\frac {\displaystyle \frac {210}{\sqrt {3}}}{\displaystyle \frac {14}{\sqrt {3}}} \\[ 5pt ]
&=&15 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,力率\( \ \cos \theta =0.8 \ \)なので,誘導性リアクタンスの大きさ\( \ X \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り,
\[
\begin{eqnarray}
X &=&Z\sin \theta \\[ 5pt ]
&=&Z\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&15\times \sqrt {1-0.8^{2} } \\[ 5pt ]
&=&9 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
負荷の抵抗の大きさ\( \ R \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り,
\[
\begin{eqnarray}
R &=&Z\cos \theta \\[ 5pt ]
&=&15\times 0.8 \\[ 5pt ]
&=&12 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
である。ここで図2の負荷について,\( \ \Delta -\mathrm {Y} \ \)変換すると,ワンポイント解説「3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,
\[
\begin{eqnarray}
R_{\mathrm {Y}} &=&\frac {R}{3} \\[ 5pt ]
&=&\frac {12}{3} \\[ 5pt ]
&=&4 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {Y}} &=&\frac {X}{3} \\[ 5pt ]
&=&\frac {9}{3} \\[ 5pt ]
&=&3 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
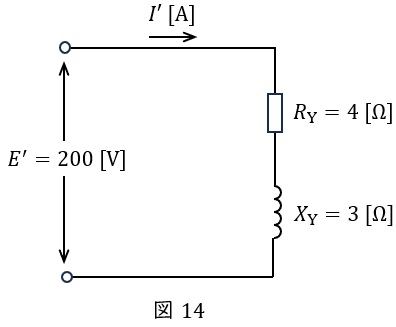
となるので,一相分等価回路は図14のように描ける。よって、線路を流れる電流\( \ I^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I^{\prime } &=&\frac {E^{\prime }}{\sqrt {{R_{\mathrm {Y}}}^{2}+{X_{\mathrm {Y}}}^{2}}} \\[ 5pt ]
&=&\frac {200}{\sqrt {4^{2}+3^{2}}} \\[ 5pt ]
&=&\frac {200}{5} \\[ 5pt ]
&=&40 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,全消費電力\( \ P^{\prime } \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P^{\prime } &=&3R_{\mathrm {Y}}{I^{\prime }}^{2} \\[ 5pt ]
&=&3\times 4 \times 40^{2} \\[ 5pt ]
&=&19 \ 200 \ \mathrm {[W]} → 19.2 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは