《電力》〈水力〉[R05下:問1]水力発電所の落差と理論式に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，水力発電の理論式に関する記述である。

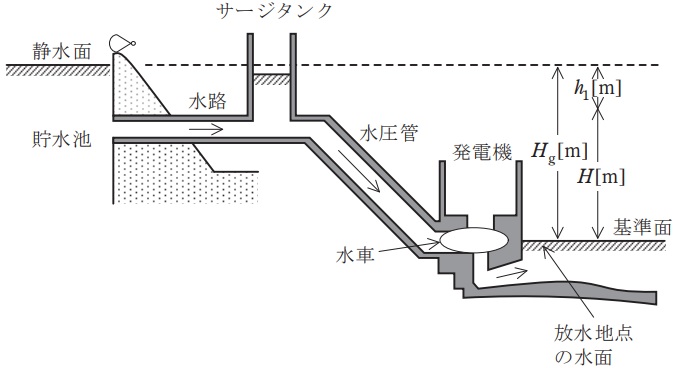
図に示すように，放水地点の水面を基準面とすれば，基準面から貯水池の静水面までの高さ\( \ H_{\mathrm {g}} \ \mathrm {[m]} \ \)を一般に\( \ \fbox {　（ア）　} \ \)という。また，水路や水圧管の壁と水との摩擦によるエネルギー損失に相当する高さ\( \ h_{\mathrm {l}} \ \mathrm {[m]} \ \)を\( \ \fbox {　（イ）　} \ \)という。さらに，\( \ H_{\mathrm {g}} \ \)と\( \ h_{\mathrm {l}} \ \)の差\( \ H=H_{\mathrm {g}} -h_{\mathrm {l}} \ \)を一般に\( \ \fbox {　（ウ）　} \ \)という。

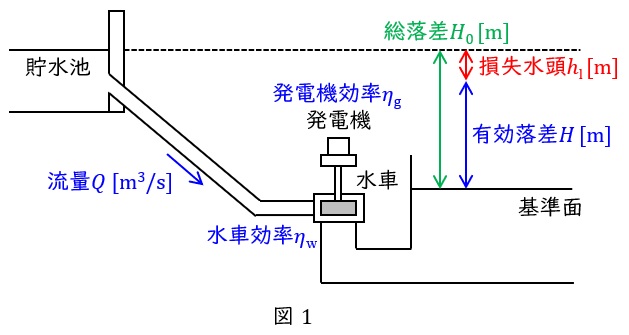
今，\( \ Q \ \mathrm {[m^{3}/s]} \ \)の水が水車に流れ込み，水車の効率を\( \ \eta _{\mathrm {w}} \ \)とすれば，水車出力\( \ P_{\mathrm {w}} \ \)は\( \ \fbox {　（エ）　} \ \)になる。さらに，発電機の効率を\( \ \eta _{\mathrm {g}} \ \)とすれば，発電機出力\( \ P \ \)は\( \ \fbox {　（オ）　} \ \)になる。ただし，重力加速度は\( \ 9.8 \ \mathrm {m/s^{2}} \ \)とする。

上記の記述中の空白箇所(ア)～(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 総落差 & 損失水頭 & 実効落差 & 9.8QH\eta _{\mathrm {w}}\times 10^{3} \ \mathrm {[W]} & 9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}}\times 10^{3} \ \mathrm {[W]} \\
\hline
(2) & 自然落差 & 位置水頭 & 有効落差 & \displaystyle \frac {9.8QH}{\eta _{\mathrm {w}}}\times 10^{-3} \ \mathrm {[kW]} & \displaystyle \frac {9.8QH\eta _{\mathrm {g}}}{\eta _{\mathrm {w}}}\times 10^{-3} \ \mathrm {[kW]} \\
\hline
(3) & 総落差 & 損失水頭 & 有効落差 & 9.8QH\eta _{\mathrm {w}}\times 10^{3} \ \mathrm {[W]} & 9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}}\times 10^{3} \ \mathrm {[W]} \\
\hline
(4) & 基準落差 & 圧力水頭 & 実効落差 & 9.8QH\eta _{\mathrm {w}} \ \mathrm {[kW]} & 9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\
\hline
(5) & 基準落差 & 速度水頭 & 有効落差 & 9.8QH\eta _{\mathrm {w}} \ \mathrm {[kW]} & 9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\
\hline
\end{array}
\]

【ワンポイント解説】

水力発電の基本式を問う定番中の定番の問題かつ非常に重要な内容となります。本問の内容は何も見なくても（オ）の公式まで導出できるようになると理想です。
本問は平成24年問1からの再出題となります。

1.水力発電所の出力\(P\)
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}／s]} \ \)，有効落差\( \ H \ \mathrm {[m]} \ \)，水車効率\( \ \eta _{\mathrm {w}} \ \)，発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると，発電機の出力\( \ P \ \mathrm {[kW]} \ \)は
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] で求められます。これは重力加速度\( \ g=9.8 \ \mathrm {[m／s^{2}]} \ \)及び水の密度\( \ \rho =1000 \ \mathrm {[kg／m^{3}]} \ \)を使用した時の発電機の出力である
\[
\begin{eqnarray}
P &=&\rho gQH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] に各値を代入し，
\[
\begin{eqnarray}
P &=&1000 \times 9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ] &=&9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] として導出したものです。

【解答】

解答：(3)
(ア)
静水面と基準面の高さの差を総落差と呼びます。

(イ)
水路や水圧管の壁と水との摩擦によるエネルギー損失に相当する高さを損失水頭と呼びます。

(ウ)
総落差から損失水頭を引いた，実際の水力発電に寄与する高さを有効落差と呼びます。

(エ)
\( \ Q \ \mathrm {[m^{3}/s]} \ \)の水が水車に流れ込んだ時の水車への入力\( \ P_{\mathrm {i}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {i}} &=&9.8QH \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] で与えられ，水車の効率が\( \ \eta _{\mathrm {w}} \ \)であるとすると，水車の出力\( \ P_{\mathrm {w}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {w}} &=&P_{\mathrm {i}}\eta _{\mathrm {w}} \\[ 5pt ] &=&9.8QH\eta _{\mathrm {w}} \ \mathrm {[kW]} \\[ 5pt ] &=&9.8QH\eta _{\mathrm {w}}\times 10^{3} \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となります。

(オ)
発電機の効率が\( \ \eta _{\mathrm {g}} \ \)であるとすると，発電機の出力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P&=&P_{\mathrm {w}}\eta _{\mathrm {g}} \\[ 5pt ] &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \times 10^{3} \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められます。

　※（エ）及び（オ）は（２）以外正答となります。