Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図のような単相\( \ 3 \ \)線式配電線路がある。系統の中間点に図のとおり負荷が接続されており,末端の\( \ \mathrm {AC} \ \)間に太陽光発電設備が逆変換装置を介して接続されている。各部の電圧及び電流が図に示された値であるとき,次の(a)及び(b)の問に答えよ。
ただし,図示していないインピーダンスは無視するとともに,線路のインピーダンスは抵抗であり,負荷の力率は\( \ 1 \ \),太陽光発電設備は発電出力電流(交流側)\( \ 15 \ \mathrm {A} \ \),力率\( \ 1 \ \)で一定とする。

(a) 図中の回路の空白箇所(ア)~(ウ)に流れる電流の値\( \ \mathrm {[A]} \ \)の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & 5 & 0 & 15 \\
\hline
(2) & 5 & 5 & 0 \\
\hline
(3) & 15 & 0 & 15 \\
\hline
(4) & 20 & 5 & 0 \\
\hline
(5) & 20 & 5 & 15 \\
\hline
\end{array}
\]
(b) 図中\( \ \mathrm {AB} \ \)間の端子電圧\( \ V_{\mathrm {AB}} \ \)の値\( \ \mathrm {[V]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 104.0 \ \) (2) \( \ 104.5 \ \) (3) \( \ 105.0 \ \) (4) \( \ 105.5 \ \) (5) \( \ 106.0 \ \)
【ワンポイント解説】
単相\( \ 3 \ \)線式線路の電流値及び電圧を求める問題です。
理解してしまえばそれほど難易度は高くないのですが,試験本番では対策をしていない受験生も多く,正答率は意外と低めとなります。特別難解な公式も使用しませんので,ぜひ中身を理解して試験本番を迎えるようにしましょう。
本問は平成19年問17からの再出題となります。
【解答】
(a)解答:(2)
(ア)
図1に示す節点\( \ \mathrm {a} \ \)には太陽光発電設備から\( \ 15 \ \mathrm {A} \ \)が入り,負荷に向かい\( \ 20 \ \mathrm {A} \ \)が出ていくので,キルヒホッフの法則の電流則より(ア)の電流値は,
\[
\begin{eqnarray}
20-15&=&5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
図1に示す節点\( \ \mathrm {b} \ \)には上の負荷から\( \ 20 \ \mathrm {A} \ \)が入り,下の負荷に\( \ 15 \ \mathrm {A} \ \)が出ていくので,キルヒホッフの法則の電流則より(イ)の電流値は,
\[
\begin{eqnarray}
20-15&=&5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(ウ)
図1に示す節点\( \ \mathrm {c} \ \)には負荷から\( \ 15 \ \mathrm {A} \ \)が入り,太陽光発電設備に向かい\( \ 15 \ \mathrm {A} \ \)が出ていくので,キルヒホッフの法則の電流則より(ウ)の電流値は,
\[
\begin{eqnarray}
15-15&=&0 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(b)解答:(4)
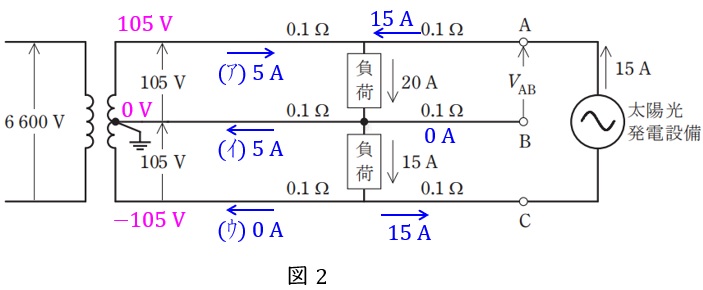
(a)の結果及び題意より,各部の電位及び電流は図2のようになる。
図2より,端子\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&105-0.1\times 5+0.1\times 15 \\[ 5pt ]
&=&106 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
であり,端子\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&0+0.1\times 5+0.1\times 0 \\[ 5pt ]
&=&0.5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {AB} \ \)間の端子電圧\( \ V_{\mathrm {AB}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {AB}}&=&V_{\mathrm {A}}-V_{\mathrm {B}} \\[ 5pt ]
&=&106-0.5 \\[ 5pt ]
&=&105.5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは