《機械》〈誘導機〉[R05下:問3]誘導機の速度制御に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，誘導機の速度制御に関する記述である。

誘導機の回転速度\( \ n \ \mathrm {[{min}^{-1}]} \ \)は，滑り\( \ s \ \)，電源周波数\( \ f \ \mathrm {[Hz]} \ \)，極数\( \ p \ \)を用いて\( \ n=120\cdot \fbox {　（ア）　} \ \)と表される。したがって，誘導機の速度は電源周波数によって制御することができ，特にかご形誘導電動機において\( \ \fbox {　（イ）　} \ \)電源装置を用いた制御が広く利用されている。

かご形誘導機ではこの他に，運転中に固定子巻線の接続を変更して\( \ \fbox {　（ウ）　} \ \)を切り換える制御法や，\( \ \fbox {　（エ）　} \ \)の大きさを変更する制御法がある。前者は，効率はよいが，速度の変化が段階的となる。後者は，速度の安定な制御範囲を広くするために\( \ \fbox {　（オ）　} \ \)の値を大きくとり，銅損が大きくなる。

巻線形誘導機では，\( \ \fbox {　（オ）　} \ \)の値を調整することにより，トルクの比例推移を利用して速度を変える制御法がある。

上記の記述中の空白箇所(ア)～(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & \displaystyle \frac {sf}{p} & \mathrm {CVCF} & 相数 & 一次電圧 & 一次抵抗 \\
\hline
(2) & \displaystyle \frac {\left( 1-s\right) f}{p} & \mathrm {CVCF} & 極数 & 二次電圧 & 二次抵抗 \\
\hline
(3) & \displaystyle \frac {sf}{p} & \mathrm {VVVF} & 極数 & 一次電圧 & 一次抵抗 \\
\hline
(4) & \displaystyle \frac {\left( 1-s\right) f}{p} & \mathrm {VVVF} & 相数 & 二次電圧 & 一次抵抗 \\
\hline
(5) & \displaystyle \frac {\left( 1-s\right) f}{p} & \mathrm {VVVF} & 極数 & 一次電圧 & 二次抵抗 \\
\hline
\end{array}
\]

【ワンポイント解説】

誘導機の速度制御に関する問題です。
同期速度の原理やトルクの比例推移等様々な知識を集約して解く問題です。全てを完璧に理解していなくても正答は導けますので，完璧主義にならないように注意してください。
本問は令和元年問4からの再出題となります。

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)，回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] と定義されます。これを整理すると，
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ] N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ] &=&\left( 1-s \right) N_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] と同期速度から回転速度が導出できます。

3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流，\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算，\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流，\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
図1より，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)，二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \)，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

4.巻線形誘導電動機のトルクの比例推移
三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T &=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ 1≫s \ \)の時，\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)以外の抵抗やリアクタンスは無視できるので，
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ] \end{eqnarray}
\] となり，トルクに対する変数は可変抵抗である二次抵抗\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)と滑り\( \ s \ \)のみであり，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)を一定とすると，
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

解答：(5)
(ア)
ワンポイント解説「2.誘導機の滑り\( \ s \ \)」より，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ] N &=&\left( 1-s\right) N_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] の関係があり，ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)」を上式に代入すると，
\[
\begin{eqnarray}
N &=&\left( 1-s\right) \frac {120f}{p} \\[ 5pt ] &=&120\cdot \frac {\left( 1-s\right) f}{p} \\[ 5pt ] \end{eqnarray}
\] と求められます。

(イ)
かご形誘導電動機で用いられている制御は\( \ \mathrm {VVVF} \ \)制御で一般にインバータ制御と呼ばれ，電圧と周波数を調整しながら制御します。\( \ \mathrm {CVCF} \ \)は無停電電源装置で，停電時に交流電力を供給するものです。

(ウ)
かご形誘導電動機では，運転中に固定子巻線の接続を変更して極数を切り換え速度を制御する方法があります。（ア）の空欄の導出の通り，極数を切り換えることにより回転速度が変わります。

(エ)
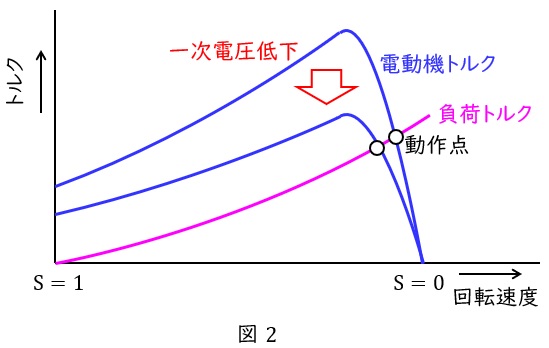
下図に示すように，かご形誘導電動機においては，一次電圧を変更することで，トルクを小さくし，動作点の滑りを大きくして速度を制御することができます。