《機械》〈電動機応用〉[R05下:問11]はずみ車に蓄えられる運動エネルギーに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

電動機ではずみ車を加速して，運動エネルギーを蓄えることを考える。

まず，加速するための電動機のトルクを考える。加速途中の電動機の回転速度を\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，そのときの毎秒の回転速度\( \ n \ \mathrm {[s^{-1}]} \ \)は①式で表される。
\[
\begin{eqnarray}
\fbox {　 （ア） 　}　・・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] この回転速度\( \ n \ \mathrm {[s^{-1}]} \ \)から②式で角速度\( \ \omega \ \mathrm {[rad／s]} \ \)を求めることができる。
\[
\begin{eqnarray}
\fbox {　 （イ） 　}　・・・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] このときの電動機が\( \ 1 \ \)秒間にする仕事，すなわち出力を\( \ P \ \mathrm {[W]} \ \)とすると，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は③式となる。
\[
\begin{eqnarray}
\fbox {　 （ウ） 　}　・・・・・・・・・・・・・・・・・　③ \\[ 5pt ] \end{eqnarray}
\] ③式のトルクによってはずみ車を加速する。電動機が出力し続けて加速している間，この分のエネルギーがはずみ車に注入される。電動機に直結するはずみ車の慣性モーメントを\( \ I \ \mathrm {[kg\cdot m^{2}]} \ \)として，加速が完了したときの電動機の角速度を\( \ \omega _{0} \ \mathrm {[rad／s]} \ \)とすると，このはずみ車に蓄えられている運動エネルギー\( \ E \ \mathrm {[J]} \ \)は④式となる。
\[
\begin{eqnarray}
\fbox {　 （エ） 　}　・・・・・・・・・・・・・・・・・　④ \\[ 5pt ] \end{eqnarray}
\] 上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　n=\displaystyle \frac {N}{60}　 & 　\omega =2\pi \times n　 & 　T=\displaystyle \frac {P}{\omega }　 & 　E=\displaystyle \frac {1}{2}I^{2}\omega _{0}　 \\
\hline
(2) & 　n=60N　 & 　\omega =\displaystyle \frac {n}{2\pi }　 & 　T=P\omega　 & 　E=\displaystyle \frac {1}{2}I^{2}\omega _{0}　 \\
\hline
(3) & 　n=\displaystyle \frac {N}{60}　 & 　\omega =2\pi \times n　 & 　T=P\omega　 & 　E=\displaystyle \frac {1}{2}I\omega _{0}^{2}　 \\
\hline
(4) & 　n=60N　 & 　\omega =\displaystyle \frac {n}{2\pi }　 & 　T=\displaystyle \frac {P}{\omega }　 & 　E=\displaystyle \frac {1}{2}I^{2}\omega _{0}　 \\
\hline
(5) & 　n=\displaystyle \frac {N}{60}　 & 　\omega =2\pi \times n　 & 　T=\displaystyle \frac {P}{\omega }　 & 　E=\displaystyle \frac {1}{2}I\omega _{0}^{2}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

はずみ車の原理に関する問題です。
近年はフライホイールという蓄電システムが確立しているので，電験でも出題されやすい問題と言えます。
本問は平成25年問10からの再出題となります。

1.出力\( \ P \ \)とトルク\( \ T \ \)の関係
一般に電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)には，角速度\( \ \omega \ \mathrm {[rad／s]} \ \)であるとき，
\[
\begin{eqnarray}
P &=& \omega T \\[ 5pt ] \end{eqnarray}
\] の関係があります。

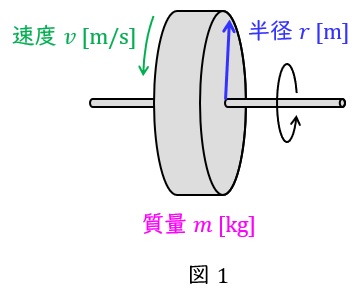
2.慣性モーメント\( \ J \ \)
質量\( \ m \ \mathrm {[kg]} \ \)，速度\( \ v \ \mathrm {[m/s]} \ \)で回転している回転体の運動エネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=& \frac {1}{2}mv^{2} \\[ 5pt ] \end{eqnarray}
\] であり，回転体の半径を\( \ r \ \mathrm {[m]} \ \)，角速度を\( \ \omega \ \mathrm {[rad/s]} \ \)とすると，\( \ v=r\omega \ \)の関係があるから，
\[
\begin{eqnarray}
W &=& \frac {1}{2}m\left( r\omega \right) ^{2} \\[ 5pt ] &=& \frac {1}{2}mr^{2}\omega ^{2} \\[ 5pt ] &=& \frac {1}{2}J\omega ^{2} \\[ 5pt ] \end{eqnarray}
\] となります。この\( \ J=mr ^{2} \ \)を慣性モーメントと呼びます。
慣性モーメントが大きいと，回転体は加速しにくく，減速しにくいという特徴があります。

【解答】

解答：(5)
(ア)
\( \ N \ \mathrm {[{min}^{-1}]} \ \)は\( \ 1 \ \)分あたりの回転速度，\( \ n \ \mathrm {[s^{-1}]} \ \)は\( \ 1 \ \)秒あたりの回転速度であるので，\( \ \displaystyle n=\frac {N}{60} \ \)となります。

(イ)
\( \ 1 \ \)回転あたりの弧度は\( \ 2\pi \ \)なので，角速度\( \ \omega \ \mathrm {[rad／s]} \ \)は，\( \ \omega =2\pi n \ \)となります。\( \ \displaystyle \omega =\frac {2\pi N}{60} \ \)も非常によく使う公式なので，暗記しておくようにしましょう。

(ウ)
ワンポイント解説「1.出力\( \ P \ \)とトルク\( \ T \ \)の関係」の通り，トルクは\( \ \displaystyle T =\frac {P}{\omega } \ \)となります。

(エ)
ワンポイント解説「2.慣性モーメント\( \ J \ \)」の通り，はずみ車に蓄えられている運動エネルギーは\( \ \displaystyle E=\displaystyle \frac {1}{2}I\omega _{0}^{2} \ \)となります。