《機械》〈同期機〉[H20:問5]同期機の内部誘導起電力の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格容量\( \ 3 \ 300 \ \mathrm {[kV\cdot A]} \ \)，定格電圧\( \ 6 \ 600 \ \mathrm {[V]} \ \)，星形結線の三相同期発電機がある。この発電機の電機子巻線の一相当たりの抵抗は\( \ 0.15 \ \mathrm {[\Omega ]} \ \)，同期リアクタンスは\( \ 12.5 \ \mathrm {[\Omega ]} \ \)である。この発電機を負荷力率\( \ 100 \ \mathrm {[％]} \ \)で定格運転したとき，一相当たりの内部誘導起電力\( \ \mathrm {[V]} \ \)の値として，最も近いのは次のうちどれか。

ただし，磁気飽和は無視できるものとする。

　(1)　\( \ 3 \ 050 \ \)　　(2)　\( \ 4 \ 670 \ \)　　(3)　\( \ 5 \ 280 \ \)　　(4)　\( \ 7 \ 460 \ \)　　(5)　\( \ 9 \ 150 \ \)

【ワンポイント解説】

同期機の内部誘導起電力を問う問題です。
ベクトル図を描いて三平方の定理を適用し解いていきます。抵抗分を無視できないのが珍しいですが，力率が\( \ 1 \ \)であるため特に問題なく解けるかと思います。

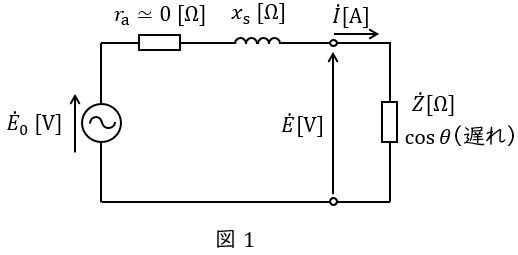
1.同期発電機の等価回路とベクトル図
同期発電機の一相分等価回路は誘導起電力（相電圧）\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)，端子電圧（相電圧）\( \ \dot E \ \mathrm {[V]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)とすると，図2のようになります。
通常，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は十分に小さいと考え，無視して考えることが一般的です。
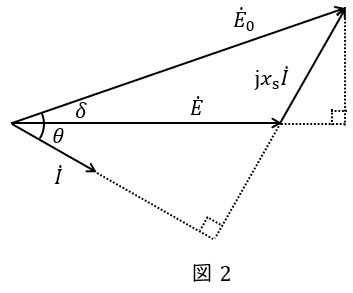
また，等価回路よりベクトル図は図3のようになります。ただし，\( \ \theta \ \)は力率角，\( \ \delta \ \)は負荷角です。

【解答】

解答：(3)
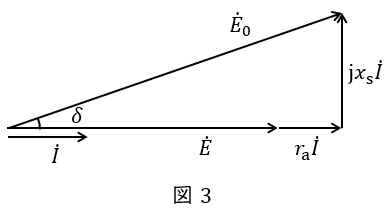
題意に沿って等価回路を描くと図3のようになる。ただし，\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)は誘導起電力（相電圧），\( \ \dot E \ \mathrm {[V]} \ \)は端子電圧（相電圧），\( \ r_{\mathrm {a}}=0.15 \ \mathrm {[\Omega ]} \ \)は電機子巻線の一相当たりの抵抗，\( \ x_{\mathrm {s}}=12.5 \ \mathrm {[\Omega ]} \ \)は同期リアクタンスである。

同期発電機の定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，定格容量\( \ P_{\mathrm {n}}=3 \ 300 \ \mathrm {[kV\cdot A]} \ \)，定格電圧\( \ V_{\mathrm {n}}=6 \ 600 \ \mathrm {[V]} \ \)なので，
\[
\begin{eqnarray}
I_{\mathrm {n}} &=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {3 \ 300\times 10^{3}}{\sqrt {3}\times 6 \ 600} \\[ 5pt ] &≒&288.7 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，図3のベクトル図に三平方の定理を適用すると，内部誘導起電力\( \ E_{0} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E_{0} &=&\sqrt {\left( E+r_{\mathrm {a}}I_{\mathrm {n}}\right) ^{2}+\left( x_{\mathrm {s}}I_{\mathrm {n}}\right) ^{2}} \\[ 5pt ] &=&\sqrt {\left( \frac {6 \ 600}{\sqrt {3}}+0.15\times 288.7\right) ^{2}+\left( 12.5\times 288.7\right) ^{2}} \\[ 5pt ] &≒&5 \ 280 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。