《機械》〈変圧器〉[R01:問8]単相変圧器の並行運転による循環電流に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

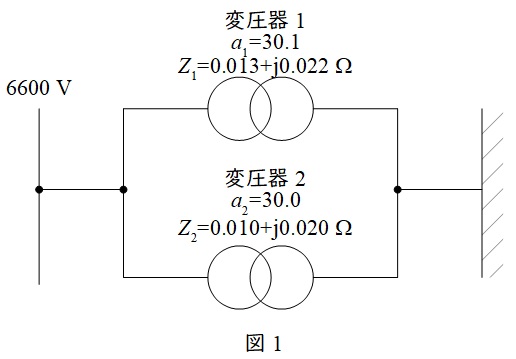
\( \ 2 \ \)台の単相変圧器があり，それぞれ，巻数比(一次巻数/二次巻数)が\( \ 30.1 \ \)，\( \ 30.0 \ \)，二次側に換算した巻線抵抗及び漏れリアクタンスからなるインピーダンスが\( \ \left( 0.013+\mathrm {j}0.022\right) \ \mathrm {\Omega } \ \)，\( \ \left( 0.010+\mathrm {j}0.020\right) \ \mathrm {\Omega } \ \)である。この\( \ 2 \ \)台の変圧器を並列接続し二次側を無負荷として，一次側に\( \ 6600 \ \mathrm {V} \ \)を加えた。この\( \ 2 \ \)台の変圧器の二次巻線間を循環して流れる電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，励磁回路のアドミタンスの影響は無視するものとする。

　(1)　\(4.1\)　　(2)　\(11.2\)　　(3)　\(15.3\)　　(4)　\(30.6\)　　(5)　\(61.3\)

【ワンポイント解説】

考え方はそれほど難しくないですが，若干計算に時間がかかる問題となっています。絶対値の計算方法や有効数字の取り方のコツ等本問にて学ぶことは結構あるので，理解しておくと良い問題となると思います。

1.変圧器の巻数比\( \ a \ \)
変圧器の一次側の巻数を\( \ N_{1} \ \)，二次側の巻数を\( \ N_{2} \ \)とすると，変圧器の巻数比\( \ a \ \)は
\[
\begin{eqnarray}
a &=&\frac {N_{1}}{N_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，一次電圧を\( \ V_{1} \ \)，一次電流を\( \ I_{1} \ \)，二次電圧を\( \ V_{2} \ \)，二次電流を\( \ I_{2} \ \)とすると，
\[
\begin{eqnarray}
a &=&\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
題意を図に示すと図1のようになり，巻数比\( \ 30.1 \ \)の変圧器を変圧器\( \ 1 \ \)，\( \ 30.0 \ \)の変圧器を変圧器\( \ 2 \ \)とし，各値を図1の通りとする。図1において，変圧器\( \ 1 \ \)及び変圧器\( \ 2 \ \)の電圧をそれぞれ\( \ V_{1} \ \)及び\( \ V_{2} \ \)とすると，
\[
\begin{eqnarray}
V_{1} &=&\frac {6600}{a_{1}} \\[ 5pt ] &=&\frac {6600}{30.1} \\[ 5pt ] &≒&219.269 \ \mathrm {[V]} \\[ 5pt ] V_{2} &=&\frac {6600}{a_{2}} \\[ 5pt ] &=&\frac {6600}{30.0} \\[ 5pt ] &=&220 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。循環電流\( \ I \ \)は二つの変圧器の電位差をそれぞれのインピーダンスで割ったものであるから，
\[
\begin{eqnarray}
I &=&\frac {V_{2}-V_{1}}{Z_{1}+Z_{2}} \\[ 5pt ] &=&\frac {220-219.269}{\left( 0.013+\mathrm {j}0.022\right) +\left( 0.010+\mathrm {j}0.020\right) } \\[ 5pt ] &=&\frac {0.731}{0.023+\mathrm {j}0.042} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさ\( \ \left| I\right| \ \)は，
\[
\begin{eqnarray}
\left| I\right| &=&\left| \frac {0.731}{0.023+\mathrm {j}0.042}\right| \\[ 5pt ] &=&\frac {0.731}{\sqrt {0.023^{2}+0.042^{2}}} \\[ 5pt ] &=&\frac {0.731}{0.04789} \\[ 5pt ] &≒&15.26　→　15.3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。