《機械》〈誘導機〉[H20:問10]交流電動機の周波数制御に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

交流電動機を駆動するとき，電動機の鉄心の\( \ \fbox {　（ア）　} \ \)を防ぎトルクを有効に発生させるために，駆動する交流基本波の電圧と周波数の比がほぼ\( \ \fbox {　（イ）　} \ \)になるようにする方法が一般的に使われている。この方法を実現する整流器とインバータによる回路とその制御の組み合わせの例には，次の二つがある。

一つの方法は，一定電圧の交流電源から直流電圧を得る整流器に\( \ \fbox {　（ウ）　} \ \)などを使用して，インバータ出力の周波数に対して目標の比となるように直流電圧を可変制御し，この直流電圧を交流に変換するインパータでは出力の周波数の調整を行う方法である。

また，別の方法は.一定電圧の交流電源から整流器を使ってほぼ一定の直流電圧を得て，インバータでは出力パルス波形を制御することによって，出力の電圧と周波数を同時に調整する方法である。

一定の直流電圧から可変の交流電圧を得るインバータの代表的な制御として，\( \ \fbox {　（エ）　} \ \)制御が知られている。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる語句として，正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　磁気飽和　 & 　一　定　 & 　ダイオード　 & 　\mathrm {PWM}　 \\
\hline
(2) & 　振　動　　 & 　2　乗　 & 　ダイオード　 & 　\mathrm {PLL}　 \\
\hline
(3) & 　磁気飽和　 & 　2　乗　 & 　サイリスタ　 & 　\mathrm {PLL}　 \\
\hline
(4) & 　振　動　　 & 　一　定　 & 　サイリスタ　 & 　\mathrm {PLL}　 \\
\hline
(5) & 　磁気飽和　 & 　一　定　 & 　サイリスタ　 & 　\mathrm {PWM}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

交流電動機の周波数制御に関する問題です。
内容は誘導機からパワーエレクトロニクスまで多岐にわたる内容なので少し難しめかもしれませんが，ある程度概要を知っていれば迷わない問題かと思います。
\( \ \mathrm {PWM} \ \)インバータのメカニズムまでは理解している必要はありませんが以下の概要については理解しておくようにして下さい。

1.三相誘導電動機の速度制御
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。また，電動機の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となり，上式を変形すると，
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ] N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ] &=&N_{\mathrm {s}}\left( 1-s\right) \\[ 5pt ] &=&\frac {120f}{p}\left( 1-s\right) \\[ 5pt ] \end{eqnarray}
\] となります。したがって，回転速度は周波数\( \ f \ \)，極数\( \ p \ \)，滑り\( \ s \ \)で制御することができます。

2.\( \ V / f \ \)一定制御
電動機の回転速度を周波数で制御する際に，電動機の磁束が飽和しないように\( \ \displaystyle \frac {V}{f} \ \)を一定とする制御です。
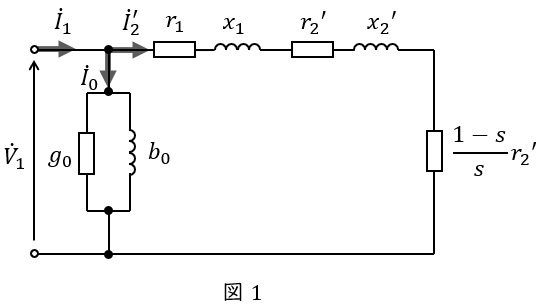
ここでは図1に示すような誘導電動機の\( \ \mathrm {L} \ \)形等価回路を用いて説明します。ただし，図1において，\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流，\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算，\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流，\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算，\( \ g_{0} \ \mathrm {[S]} \ \)は励磁コンダクタンス，\( \ b_{0} \ \mathrm {[S]} \ \)は励磁サセプタンス，\( \ s \ \)は滑りとなります。
界磁磁束\( \ \mathit {\Phi } \ \mathrm {[Wb]} \ \)は励磁電流\( \ I_{0} \ \mathrm {[A]} \ \)に比例し，図1において，励磁電流\( \ I_{0} \ \mathrm {[A]} \ \)は\( \ g_{0} \ \mathrm {[S]} \ \)が小さいとすると\( \ b_{0} \ \mathrm {[S]} \ \)にほぼ比例します。
\( \ \displaystyle b_{0}=\frac {1}{2\pi fL} \ \)であり，\( \ b_{0} \ \mathrm {[S]} \ \)は周波数\( \ f \ \mathrm {[Hz]} \ \)に反比例するので，磁束\( \ \mathit {\Phi } \ \mathrm {[Wb]} \ \)は周波数\( \ f \ \mathrm {[Hz]} \ \)にほぼ反比例することがわかります。
また，図1の等価回路において，オームの法則より励磁電流\( \ I_{0} \ \mathrm {[A]} \ \)は\( \ V_{1} \ \mathrm {[V]} \)に比例するので，磁束\( \ \mathit {\Phi } \ \mathrm {[Wb]} \ \)は\( \ \displaystyle \frac {V}{f} \ \)にほぼ比例することが分かります。
したがって，磁束を飽和させないためには周波数を変動させると同時に電圧を変化させる必要があることがわかります。

3.\( \ \mathrm {PWM} \ \)制御
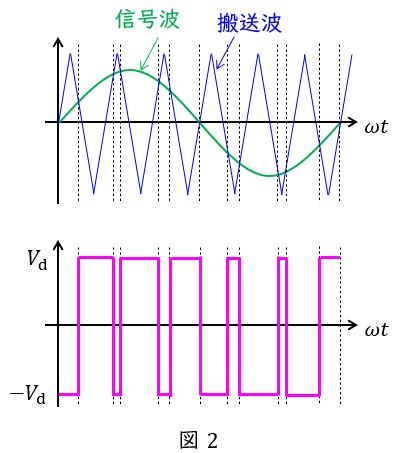
三相ブリッジインバータ等を用いて，信号波と高周波の搬送波を比較し，出力電圧をパルス幅で調整する方法です。
図2の例においては信号波＞搬送波のとき\( \ V_{\mathrm {d}} \ \)を出力，\( \ V_{\mathrm {d}} \ \)を出力してパルス幅により出力電圧を調整しています。
そして，信号波を\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずらしてオンオフ制御することで出力に可変の電圧と周波数の三相交流を得ることができます。