Contents
【問題】
【難易度】★★★★☆(やや難しい)
平衡三相回路について,次の(a)及び(b)に答えよ。
(a) 図1のように,抵抗\( \ R \ \)とコイル\( \ L \ \)からなる平衡三相負荷に,線間電圧\( \ 200 \ \mathrm {[V]} \ \),周波数\( \ 50 \ \mathrm {[Hz]} \ \)の対称三相交流電源を接続したところ,三相負荷全体の有効電力は\( \ P= 2.4 \ \mathrm {[kW]} \ \)で,無効電力は\( \ Q= 3.2 \ \mathrm {[kvar]} \ \)であった。負荷電流\( \ I \ \mathrm {[A]} \ \)の値として,最も近いのは次のうちどれか。
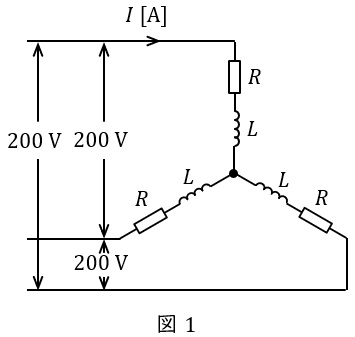
(1) \( \ 2.3 \ \) (2) \( \ 4.0 \ \) (3) \( \ 6.9 \ \) (4) \( \ 9.2 \ \) (5) \( \ 11.5 \ \)
(b) 図1に示す回路の各線間に同じ静電容量のコンデンサ\( \ C \ \)を図2に示すように接続した。このとき,三相電源からみた力率が\( \ 1 \ \)となった。このコンデンサ\( \ C \ \)の静電容量\( \ \mathrm {[\mu F]} \ \)の値として,最も近いのは次のうちどれか。
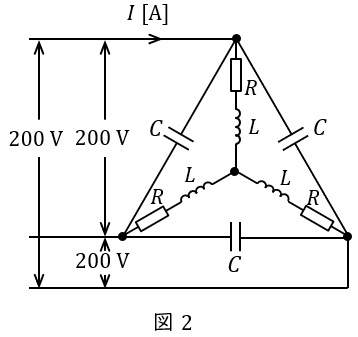
(1) \( \ 48.8 \ \) (2) \( \ 63.4 \ \) (3) \( \ 84.6 \ \) (4) \( \ 105.7 \ \) (5) \( \ 146.5 \ \)
【ワンポイント解説】
三相交流回路の回路演算を行う問題です。
本問は様々な解法が考えられますが,ご自身で正答が導き出せれば特に問題はありませんので,解答や別解を参考にご自身の解き方を確立していくようにして下さい。
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
となります。この関係をベクトル図に表すと,図3~図5となります。
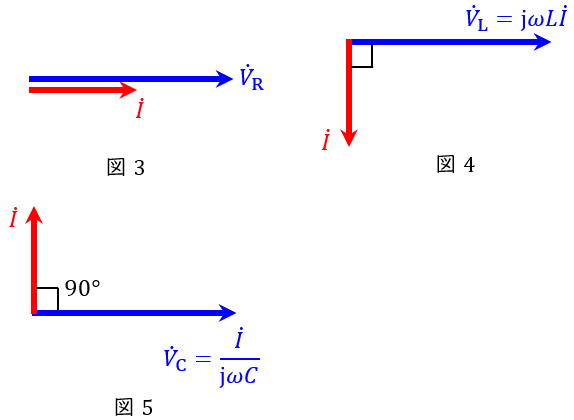
2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
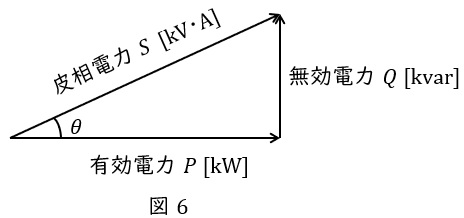
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \),リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び,図6のようにベクトル図を描きます。さらに,有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図6において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
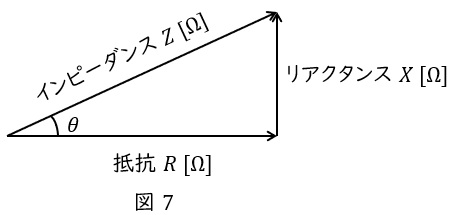
また,線路に電流\( \ I \ \mathrm {[A]} \ \)が流れているとき,皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \),有効電力\( \ P \ \mathrm {[W]} \ \),無効電力\( \ Q \ \mathrm {[var]} \ \)は,インピーダンスを\( \ Z \ \mathrm {[\Omega ]} \ \),抵抗を\( \ R \ \mathrm {[\Omega ]} \ \),リアクタンスを\( \ X \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ]
P &=&RI^{2} \\[ 5pt ]
Q &=&XI^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ Z \ \mathrm {[\Omega ]} \ \),\( \ R \ \mathrm {[\Omega ]} \ \),\( \ X \ \mathrm {[\Omega ]} \ \)に関しても電力と同様な図7のような関係を描くことができます。
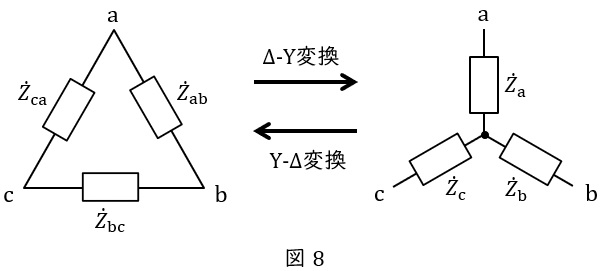
3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図8において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図8において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(5)
有効電力\( \ P \ \mathrm {[W]} \ \)を求める式を変形すると,
\[
\begin{eqnarray}
P &=&\sqrt {3}VI\cos \theta \\[ 5pt ]
&=&\sqrt {3}VI\cdot \frac {P}{\sqrt {P^{2}+Q^{2}}} \\[ 5pt ]
1&=&\sqrt {3}VI\cdot \frac {1}{\sqrt {P^{2}+Q^{2}}} \\[ 5pt ]
I&=&\frac {\sqrt {P^{2}+Q^{2}}}{\sqrt {3}V} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入すれば,
\[
\begin{eqnarray}
I&=&\frac {\sqrt {\left( 2.4\times 10^{3}\right) ^{2}+\left( 3.2\times 10^{3}\right) ^{2}}}{\sqrt {3}\times 200} \\[ 5pt ]
&≒&11.547 → 11.5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[別解]
皮相電力\( \ S \ \mathrm {[kV\cdot A]} \ \)を求める式より,
\[
\begin{eqnarray}
S=\sqrt {P^{2}+Q^{2}} &=&\sqrt {3}VI \\[ 5pt ]
I &=&\frac {\sqrt {P^{2}+Q^{2}} }{\sqrt {3}V} \\[ 5pt ]
&=&\frac {\sqrt {\left( 2.4\times 10^{3}\right) ^{2}+\left( 3.2\times 10^{3}\right) ^{2}}}{\sqrt {3}\times 200} \\[ 5pt ]
&≒&11.547 → 11.5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
コンデンサ\( \ C \ \mathrm {[F]} \ \)を\( \ \Delta -\mathrm {Y} \ \)変換すると,ワンポイント解説「3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,
\[
\begin{eqnarray}
X_{\mathrm {Y}}&=&\frac {1}{3}\cdot \frac {1}{2\pi fC} \\[ 5pt ]
&=&\frac {1}{2\pi f\left( 3C\right) } \\[ 5pt ]
\end{eqnarray}
\]
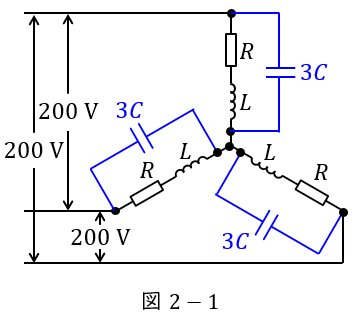
となるので,図2は図2-1のように書き換えられる。このときの力率が\( \ 1 \ \)なので,コンデンサ全体で消費される進み無効電力が\( \ Q= 3.2 \ \mathrm {[kvar]} \ \)であることから,
\[
\begin{eqnarray}
Q&=&3\cdot \frac {\displaystyle \left( \frac {200}{\sqrt {3}}\right) ^{2}}{X_{\mathrm {Y}}} \\[ 5pt ]
&=&3\cdot \frac {\displaystyle \frac {40 \ 000}{3}}{\displaystyle \frac {1}{2\pi f\left( 3C\right) } } \\[ 5pt ]
&=&\frac {40 \ 000 }{\displaystyle \frac {1}{6\pi fC} } \\[ 5pt ]
&=&40 \ 000 \times 6\pi fC \\[ 5pt ]
3.2\times 10^{3}&=&40 \ 000 \times 6\pi \times 50\times C \\[ 5pt ]
C&=&\frac {3.2\times 10^{3}}{40 \ 000 \times 6\pi \times 50} \\[ 5pt ]
&≒&84.9\times 10^{-6} \ \mathrm {[F]} → 84.9 \ \mathrm {[\mu F]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[別解]
各コンデンサに加わる電圧が\( \ 200 \ \mathrm {[V]} \ \)であり,コンデンサ全体で消費される進み無効電力が\( \ Q= 3.2 \ \mathrm {[kvar]} \ \)であるから,
\[
\begin{eqnarray}
Q&=&3\cdot \frac {200^{2}}{\displaystyle \frac {1}{2\pi f C}} \\[ 5pt ]
&=&3\cdot 2\pi f C\times 40 \ 000 \\[ 5pt ]
3.2\times 10^{3}&=&3\times 2 \pi \times 50\times C\times 40 \ 000 \\[ 5pt ]
C&=&\frac {3.2\times 10^{3}}{3\times 2\pi \times 50\times 40 \ 000 } \\[ 5pt ]
&≒&84.9\times 10^{-6} \ \mathrm {[F]} → 84.9 \ \mathrm {[\mu F]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは