《理論》〈電子理論〉[H19:問17]導体中を流れる自由電子の移動速度に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

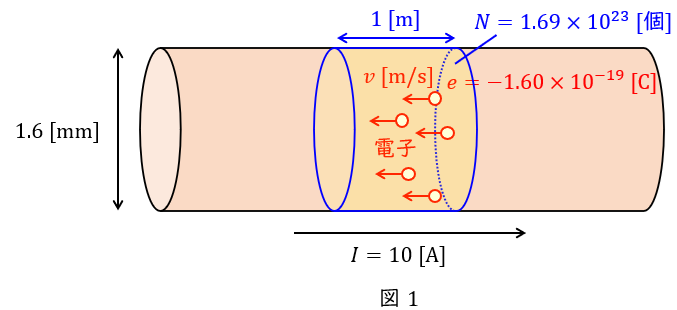
直径\( \ 1.6 \ \mathrm {[mm]} \ \)の銅線中に\( \ 10 \ \mathrm {[A]} \ \)の直流電流が一様に流れている。この銅線の長さ\( \ 1 \ \mathrm {[m]} \ \)当たりの自由電子の個数を\( \ 1.69\times 10^{23} \ \)個，自由電子\( \ 1 \ \)個の電気量を\( \ -1.60 \times 10^{-19} \ \mathrm {[C]} \ \)として，次の(a)及び(b)に答えよ。

なお，導体中の直流電流は自由電子の移動によってもたらされているとみなし，その移動の方向は電流の方向と逆である。

また，ある導体の断面を\( \ 1 \ \)秒間に\( \ 1 \ \mathrm {[C]} \ \)の割合で電荷が通過するときの電流の大きさが\( \ 1 \ \mathrm {[A]} \ \)と定義される。

(a)　\( \ 10 \ \mathrm {[A]} \ \)の直流電流が流れているこの銅線の中を移動する自由電子の平均移動速度\( \ v \ \mathrm {[m / s]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 1.37 \times 10^{-7} \ \)　　(2)　\( \ 3.70 \times 10^{-4} \ \)　　(3)　\( \ 1.92 \times 10^{-2} \ \)
　(4)　\( \ 1.84 \times 10^{2} \ \)　　(5)　\( \ 3.00 \times 10^{8} \ \)

(b)　この銅線と同じ材質の銅線の直径が\( \ 3.2 \ \mathrm {[mm]} \ \)，流れる直流電流が\( \ 30 \ \mathrm {[A]} \ \)であるとき，自由電子の平均移動速度\( \ \mathrm {[m / s]} \ \)は左記(a)の速度の何倍になるか。その倍数として，最も近いのは次のうちどれか。
なお，銅線の単位体積当たりの自由電子の個数は同一である。

　(1)　\( \ 0.24 \ \)　　(2)　\( \ 0.48 \ \)　　(3)　\( \ 0.75 \ \)　　(4)　\( \ 6.0 \ \)　　(5)　\( \ 12 \ \)

【ワンポイント解説】

導体中を流れる自由電子の移動速度を考える問題です。
試験本番で問題文を読解する能力が求められる\( \ 2 \ \)種以上で出題されやすいパターンの問題です。あまり電験では出題されていない内容で，参考書の掲載も少ない内容かと思います。

1.電流の定義
電流は導体の断面を単位時間当たりに通過する電荷量で定義され，\( \ \Delta t \ \mathrm {[s]} \ \)の間に\( \ \Delta Q \ \mathrm {[C]} \ \)の電荷が通過するときの電流の大きさ\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I &=&\frac {\Delta Q}{\Delta t} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(2)
銅線\( \ 1 \ \mathrm {[m]} \ \)当たりの電気量\( \ q \ \mathrm {[C / m]} \ \)は，
\[
\begin{eqnarray}
q &=&1.69\times 10^{23}\times 1.60\times 10^{-19} \\[ 5pt ] &=&27 \ 040 \ \mathrm {[C / m]} \\[ 5pt ] \end{eqnarray}
\] であり，電流\( \ I=10 \ \mathrm {[A]} \ \)の流れで電子が平均\( \ v \ \mathrm {[m / s]} \ \)で\( \ t \ \mathrm {[s]} \ \)移動したとすると，移動した電気量を求める式から，
\[
\begin{eqnarray}
It &=&qvt \\[ 5pt ] I &=&qv \\[ 5pt ] v &=&\frac {I}{q} \\[ 5pt ] &=&\frac {10}{27 \ 040} \\[ 5pt ] &≒&3.698\times 10^{-4}　→　3.70\times 10^{-4} \ \mathrm {[m / s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
直径\( \ 3.2 \ \mathrm {[mm]} \ \)の銅線\( \ 1 \ \mathrm {[m]} \ \)当たりの電気量\( \ q^{\prime } \ \mathrm {[C / m]} \ \)は，断面積が\( \ 4 \ \)倍であるから，
\[
\begin{eqnarray}
q^{\prime } &=&4q \\[ 5pt ] &=&4\times 27 \ 040 \\[ 5pt ] &=&108 \ 160 \ \mathrm {[C / m]} \\[ 5pt ] \end{eqnarray}
\] であり，電流\( \ I^{\prime }=30 \ \mathrm {[A]} \ \)の流れで電子が平均\( \ v^{\prime } \ \mathrm {[m / s]} \ \)で\( \ t \ \mathrm {[s]} \ \)移動したとすると，移動した電気量を求める式から，
\[
\begin{eqnarray}
I^{\prime }t &=&q^{\prime }v^{\prime }t \\[ 5pt ] I^{\prime } &=&q^{\prime }v^{\prime } \\[ 5pt ] v^{\prime } &=&\frac {I^{\prime }}{q^{\prime }} \\[ 5pt ] &=&\frac {30}{108 \ 160} \\[ 5pt ] &≒&2.774 \times 10^{-4} \ \mathrm {[m / s]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ v=3.698\times 10^{-4} \ \mathrm {[m / s]} \ \)との比は，
\[
\begin{eqnarray}
\frac {v^{\prime }}{v} &=&\frac {2.774 \times 10^{-4}}{3.698\times 10^{-4}} \\[ 5pt ] &≒&0.75 \\[ 5pt ] \end{eqnarray}
\] と求められる。

[別解]
直径が(a)の\( \ 2 \ \)倍なので断面積は(a)の\( \ 4 \ \)倍となるから，同じ電流での自由電子の平均移動速度は\( \ \displaystyle \frac {1}{4} \ \)倍となる。
電流は(a)の\( \ 3 \ \)倍なので，同じ断面積での自由電子の平均移動速度は(a)の\( \ 3 \ \)倍となる。
よって，これらを組み合わせて平均移動速度は\( \ \displaystyle \frac {1}{4}\times 3=0.75 \ \)倍と求められる。