《機械》〈パワーエレクトロニクス〉[H19:問9]入力波形からの適切な電力変換回路の選定に関する選択問題

【問題】

【難易度】★★★☆☆（普通）

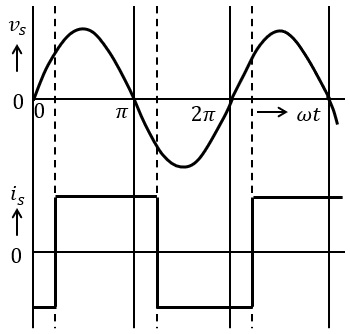
入力交流電圧波形\( \ v_{s} \ \)に対し，図のような入力電流波形\( \ i_{s} \ \)となる電力変換回路として，正しいのは次のうちどれか。

ただし，交流電源のインピーダンスは無視できるものとし，電力変換回路における平滑リアクトルは十分に大きなインダクタンスを持っているものとする。

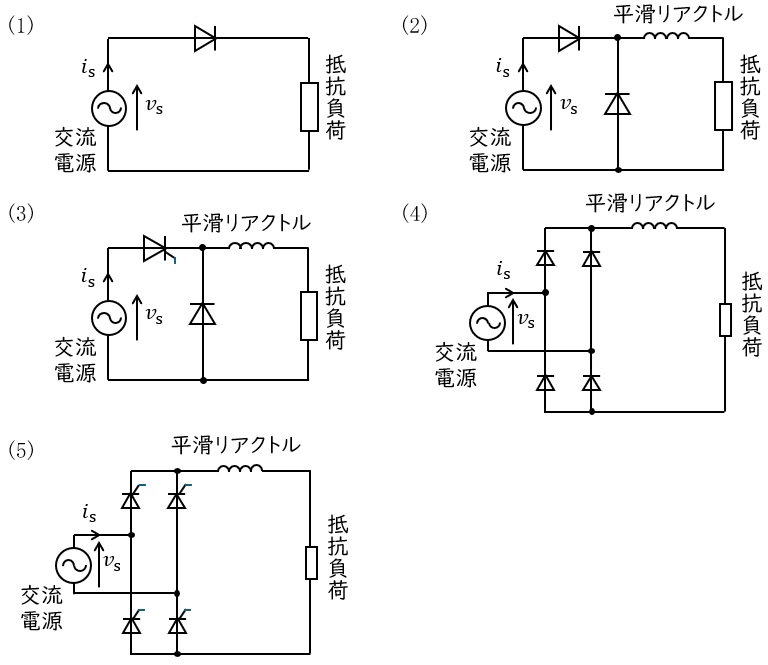
【ワンポイント解説】

入力電圧波形と入力電力波形から正しい整流回路を選択する問題です。
動作メカニズムを理解していれば正答を導き出すことができますが，総じて受験生の正答率は低い問題です。
一度理解してしまえば忘れにくい内容なので，本問で各回路の動作原理を理解するようにしましょう。

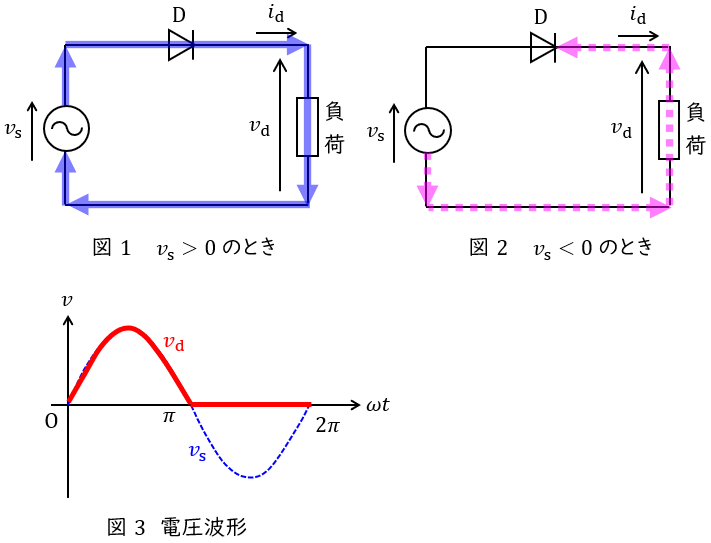
1.単相半波ダイオード整流回路の動作
単相半波ダイオード整流回路の動作を図1及び図2に示します。
正弦波の電源電圧\( \ v_{\mathrm {s}} ＞ 0 \ \)のときは，図1のようにダイオード\( \ \mathrm {D} \ \)が導通するため，出力側に電流が流れますが，電源電圧\( \ v_{\mathrm {s}} ＜ 0 \ \)に切り換わると，ダイオード\( \ \mathrm {D} \ \)に対し逆方向の電圧が加わるため\( \ \mathrm {D} \ \)が導通せず，電流は流れなくなります。
したがって，出力電圧の波形は図3のようになり，整流されることになります。
平均出力電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は，交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {d}} &=& \frac {1}{2\pi }\int _{0}^{\pi }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {\sqrt {2}}{2\pi }V\left[ -\cos \omega t\right] _{0}^{\pi } \\[ 5pt ] &=& \frac {\sqrt {2}}{2\pi }V\left( -\cos \pi +\cos 0 \right) \\[ 5pt ] &=& \frac {\sqrt {2}}{2\pi }V\left\{ -\left( -1 \right) +1 \right\} \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V \\[ 5pt ] &≃& 0.45V \\[ 5pt ] \end{eqnarray}
\] となります。

※積分の考え方を使用しているので，\( \ 3 \ \)種としては結果を暗記することになります。

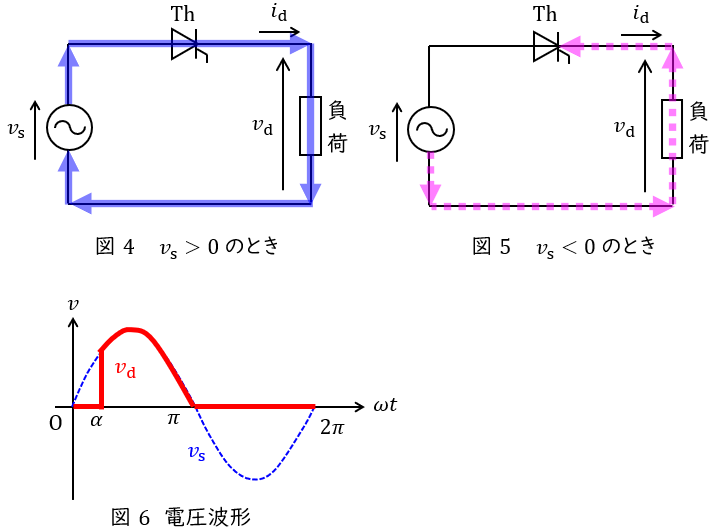
2.単相半波サイリスタ整流回路の動作
単相半波サイリスタ整流回路の動作を図4及び図5に示します。
基本的な動作はダイオードと同じですが，サイリスタにはゲートによるターンオン制御が可能であるため，制御角\( \ \alpha \ \mathrm {[rad]} \ \)により出力平均電圧を調整することができます。
したがって，出力電圧の波形は図6のようになります。

平均出力電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は，交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {d}} &=& \frac {1}{2\pi }\int _{\alpha }^{\pi }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {\sqrt {2}}{2\pi }V\left[ -\cos \omega t\right] _{\alpha }^{\pi } \\[ 5pt ] &=& \frac {\sqrt {2}}{2\pi }V\left( -\cos \pi +\cos \alpha \right) \\[ 5pt ] &=& \frac {\sqrt {2}}{2\pi }V\left\{ -\left( -1 \right) +\cos \alpha \right\} \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\frac {1+\cos \alpha }{2} \\[ 5pt ] &≃& 0.45V\frac {1+\cos \alpha }{2}
\end{eqnarray}
\] となります。

※積分の考え方を使用しているので，\( \ 3 \ \)種としては結果を暗記することになります。

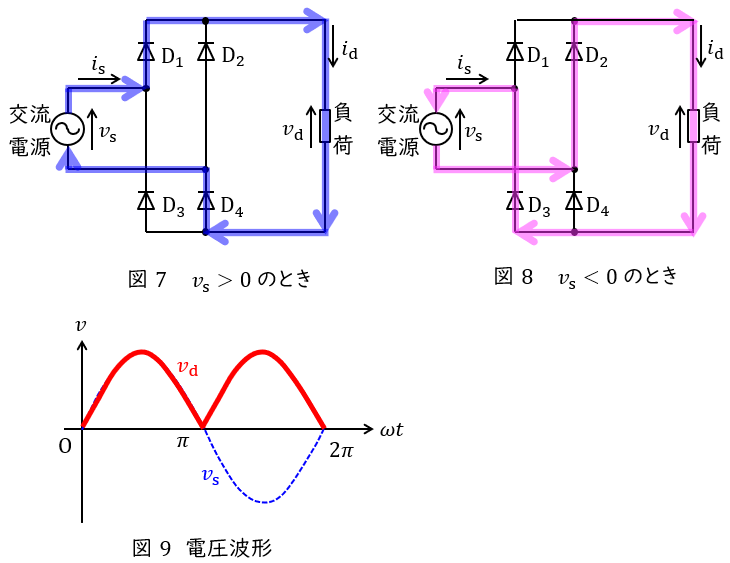
3.単相ダイオードブリッジ整流回路の動作
図7，図8に示す単相ダイオードブリッジ整流回路は以下のように動作します。

①\( \ v_{\mathrm {s}}＞0 \ \)のとき
図7のように，電流は交流電源→\( \ \mathrm {D}_{1} \ \)→負荷→\( \ \mathrm {D}_{4} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると，入力電圧\( \ v_{\mathrm {s}} \ \)と等しくなります。

②\( \ v_{\mathrm {s}}＜0 \ \)のとき
図8のように，電流は交流電源→\( \ \mathrm {D}_{2} \ \)→負荷→\( \ \mathrm {D}_{3} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると，\( \ -v_{\mathrm {s}} \ \)となります。

したがって，出力電圧の波形は図9のようになります。
図9より平均出力電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は，交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {d}} &=& \frac {1}{\pi }\int _{0}^{\pi }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left[ -\cos \omega t\right] _{0}^{\pi } \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left( -\cos \pi +\cos 0 \right) \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left\{ -\left( -1 \right) +1 \right\} \\[ 5pt ] &=& \frac {2\sqrt {2}}{\pi }V \\[ 5pt ] &≃& 0.90V \\[ 5pt ] \end{eqnarray}
\] となります。

※積分の考え方を使用しているので，\( \ 3 \ \)種としては結果を暗記することになります。

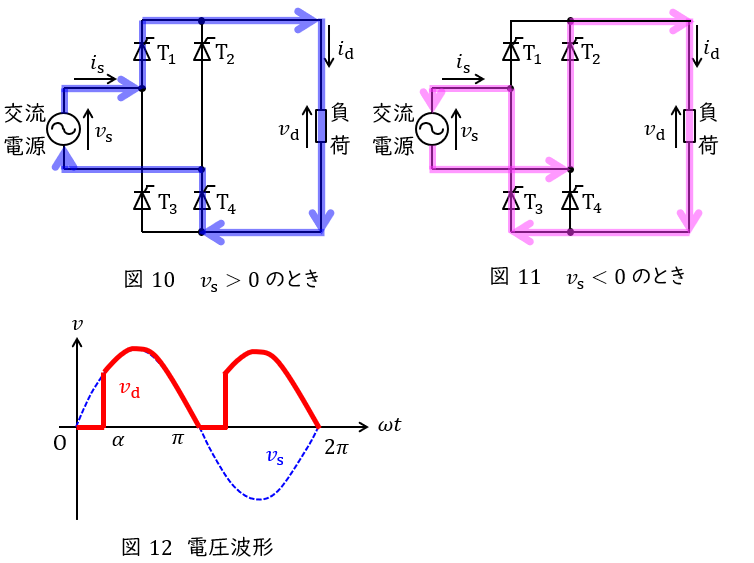
4.単相サイリスタブリッジ整流回路の動作
図10，図11に示す単相サイリスタブリッジ整流回路は以下のように動作します。

①\( \ v_{\mathrm {s}}＞0 \ \)でサイリスタ\( \ \mathrm {T}_{1} \ \)と\( \ \mathrm {T}_{4} \ \)がオンとなったとき
図10のように，電流は交流電源→\( \ \mathrm {T}_{1} \ \)→負荷→\( \ \mathrm {T}_{4} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると，入力電圧\( \ v_{\mathrm {s}} \ \)と等しくなります。

②\( \ v_{\mathrm {s}}＜0 \ \)でサイリスタ\( \ \mathrm {T}_{2} \ \)と\( \ \mathrm {T}_{3} \ \)がオンとなったとき
図11のように，電流は交流電源→\( \ \mathrm {T}_{2} \ \)→負荷→\( \ \mathrm {T}_{3} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると，\( \ -v_{\mathrm {s}} \ \)となります。

サイリスタにはゲートによるターンオン制御が可能であるため，制御角\( \ \alpha \ \mathrm {[rad]} \ \)により出力電圧の波形は図12のようになります。図12より，制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)で制御しているとすると平均出力電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は，交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {d}} &=& \frac {1}{\pi }\int _{\alpha }^{\pi }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left[ -\cos \omega t\right] _{\alpha }^{\pi } \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left( -\cos \pi +\cos \alpha \right) \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left\{ -\left( -1\right) +\cos \alpha \right\} \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left( 1 +\cos \alpha \right) \\[ 5pt ] &=& \frac {2\sqrt {2}}{\pi }V\frac {1+\cos \alpha }{2} \\[ 5pt ] &≃& 0.90V\frac {1+\cos \alpha }{2} \\[ 5pt ] \end{eqnarray}
\] となります。

※積分の考え方を使用しているので，\( \ 3 \ \)種としては結果を暗記することになります。

【解答】

解答：(5)
各ワンポイント解説の通り，各選択肢の回路は，
　(1)：単相半波ダイオード整流回路
　(2)：（平滑リアクトルと還流ダイオードを含む）単相半波ダイオード整流回路
　(3)：単相半波サイリスタ整流回路
　(4)：単相全波ダイオード整流回路
　(5)：単相全波サイリスタ整流回路
であり，問題の波形は，電流が制御角\( \ \alpha \ \)で正負が入れ替わるので，サイリスタを使用した全波整流回路であることがわかる。
したがって，回路として適切なのは(5)と求められる。